IEMDaily - Video Lecture Notes

Definition

Explain refraction of sound

Refraction of sound waves is most evident in situations in which the sound wave passes through a medium with gradually varying properties. For example, sound waves are known to refract when traveling over water. Even though the sound wave is not exactly changing media, it is traveling through a medium with varying properties; thus, the wave will encounter refraction and change its direction.

Example

Infer reflected and transmitted waves at a boundary for a composite wave

Example: A composition string is made up by joining two strings of different masses per unit length

⟶ μ

and

4 μ .

The composite string is under the same tension. A transverse wave pulse: Y=(6 mm) sin (5t+40x), where 't' is in seconds and 'x' in meters, is sent along the lighter string towards the joint. The joint is at x=0. Find the equation of the wave pulse reflected from the joint.

Solution:
Since the wave is travelling from low to more dense medium, thus there will be inversion of the reflected wave . Since it travels back from origin, thus 40x will become -40x. Also, amplitude of reflected wave is given by:

A_{r} = \frac{Z_{1} - Z_{2}}{Z_{1} + Z_{2}} A . Z = μ c = μ \sqrt{\frac{T}{μ}} = \sqrt{μ T}

Z=characteristic impedence of string,

Z_{1}

= characteristic impedence of string 1,

Z_{2}

= characteristic impedence of string 2
Thus

A_{r} = \frac{\sqrt{μ T} - \sqrt{4 μ T}}{\sqrt{μ T} + \sqrt{4 μ T}} A = \frac{- 1}{3} A

Thus it become

\frac{- 6}{3} = - 2

.
So, the equation becomes: -2sin(5t-40x)

Example

Write the equation of reflected wave for a given incident wave at an open boundary

Example: Find the equation of reflected wave from an open boundary.

Solution:
When a wave reflects from an open boundary, the wave retains its shape.
Equation of incident wave:

y = A c o s (k x + ω t)

Equation of reflected wave from open boundary:

y_{r} = A c o s (k x - ω t)

Result

Infer reflected wave on a string on reflection from an open boundary

In an open pipe, when a compressed wave reaches the far end, the air at that point is, for an instant, at a pressure greater than the atmospheric pressure. Being an open end, the air there can vibrate with maximum freedom and so, it suddenly expands into the surrounding air. Thus, the pressure diminishes so quickly that it becomes lesser than the pressure of the surrounding air, which causes a sudden rarefaction at the end of the pipe. This sets up a rarefied wave which passes back along the pipe. Within the tube, the reflected pulses meet the direct ones and the result is the formation of the standing wave.

Example

Find the nodes of a given sinusoidal standing wave on a string fixed at one end

Example:
A wave of length

2 m

is superposed on its reflected wave to form a stationary wave. A node is located at

3 x = 3 m

. Find the location of the next node.

Solution:
Since wave length is

2 m

, half of wavelength is

1 m

. Node forms after each half of wave length. So, node will be formed at each

1 m

.
So, as node is formed at

3 m

next node will be formed at

3 + 1 = 4 m .

Definition

Anti-node of a given sinusoidal standing wave on a string fixed at one end

We can analyze a situation by considering wave functions for two transverse sinusoidal waves having the same amplitude, frequency, and wavelength but traveling in opposite directions in the same medium:

y_{1} = A s i n (k x - ω t

y_{2} = A s i n (k x + ω t

Resultant

y = y_{1} + y_{2} = (2 A s i n k x) c o s ω t

The positions in the medium at which this maximum displacement occurs are called antinodes. The antinodes are located at positions for which the coordinate x satisfies the condition

s i n k x = 1

, that is, when

k x = \frac{π}{2}, \frac{3 π}{2}, \frac{5 π}{2}, . . . . . .

Position of antinodes

x = \frac{λ}{4}, \frac{3 λ}{4}, \frac{5 λ}{4}, . . . . = \frac{n λ}{4} n = 1, 3, 5, . . . .

Example

Use force analysis to find formula for velocity of transverse wave on a string

Example: The mass of a

4 m

long string is

0.01 k g

. It is stretched by a force of

400 N

. Find the velocity of the transverse wave propagating in the string?

Solution:
The velocity of the transverse wave propagating in the string is:

T e n s i o n (T) = 400 N

Mass per unit length

(μ) =

Mass of string/length of string =

\frac{0.01}{4}

v = \sqrt{\frac{T}{μ}} = \sqrt{\frac{400}{\frac{0.01}{4}}} = 400

m/s

Example

Mechanical Resonance

Various examples of mechanical resonance include:
     1. musical instruments (acoustic resonance).
   2. Most clocks keep time by mechanical resonance in a balance wheel,   pendulum, or quartz crystal.
   3. Tidal resonance of the Bay of Fundy.
   4. Orbital resonance as in some moons of the solar system's gas giants.
   5. The resonance of the basilar membrane in the ear.
   6. Making a child's swing swing higher by pushing it at each swing.
   7. A wineglass breaking when someone sings a loud note at exactly the right   pitch.

Example

Acoustic Resonance

1. The classic example of this is breaking a wine glass with sound at the precise resonant frequency of the glass; although this is difficult in practice.

2. Resonance of a stiff structural element called the basilar membrane within the cochlea of the inner ear allows hair cells on the membrane to detect sound.

Example

Demonstration of resonance with pendulums

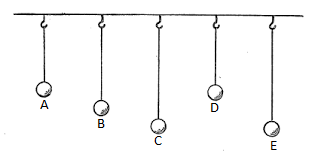
Resonance and forced vibrations can be demonstrated using a set of pendulums. Five pendulums A, B, C, D and E are suspended vertically from the same horizontal support as shown in the figure. Lengths of A and D are equal and hence their individual frequency of oscillations are equal. Pendulum A is now displaced to one side and hence set into motion. After some time, pendulum D starts vibrating and soon gains some amplitude. After some time, all energy of A is transferred to D and vibration amplitude of D becomes maximum while that of A is minimum. The exchange of energy takes place continuously. Other pendulums also oscillate with a smaller magnitude.