Wave Motion and String Waves Concept Page - 8

Example

Use condition on path difference for two superimposing sound waves for constructive interference

Example: In a large room, a person receives direct sound waves from a source 120 m$120m$ away from him. He also receives waves from the 25 m$25m$ high ceiling at a point half way between them. For which wavelengths the two waves interfere constructively?

Solution:
Path difference is Δx$\mathrm{\Delta }x$

Δx=2[252+602−−−−−−−−√]−120=10 m$\mathrm{\Delta }x=2[\sqrt{{25}^2+{60}^2}]-120=10m$
phase change δ=2πλΔx$\delta ={\displaystyle \frac{2\pi }{\lambda }}\mathrm{\Delta }x$

Constructive interference for δ=2nπ$\delta =2n\pi$, where n=1,2,3$n=1,2,3$ etc.
Thus, λ1=10 m${\lambda }_1=10m$ for n=1$n=1$
λ2=5 m${\lambda }_2=5m$ for n=2$n=2$
λ3=10/3 m${\lambda }_3=10/3m$ for n=3$n=3$ etc.

Definition

Define destructive interference and state condition on phase difference for destructive interference

If a crest of one wave meets a trough of another wave then the magnitude of the displacements is equal to the difference in the individual magnitudes this is known as destructive interference. For destructive interference  Δx=(2n+1)λ2=(2n+1)2vf${\displaystyle \mathrm{\Delta }x=(2n+1)\frac{\lambda }{2}=\frac{(2n+1)}{2}\frac{v}{f}}$ where n=1,2,.....

Example

Use condition on path difference for two superimposing sound waves for destructive interference

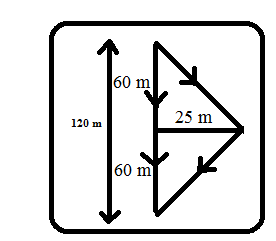
Example: Two small loud speakers A$A$ and B$B$ are driven by the same amplifier as shown in figure and emit pure sinusoidal waves in phase. Speaker A$A$ is 1 m$1m$ away as shown and speaker B$B$ is 2 m$2m$ away from the amplifier. The microphone is 4 m$4m$ away from the amplifier in transverse direction as indicated in the figure.Speed of sound is 350 m/s$350m/s$.

Solution:
Path difference between sound from the sources meeting at P=42+22−−−−−−√−42+12−−−−−−√=0.35m$\sqrt{4^2+2^2}-\sqrt{4^2+1^2}=0.35m$
For destructive interference, path difference=(n+12)λ=(n+12)cν$(n+{\displaystyle \frac{1}{2}})\lambda =(n+{\displaystyle \frac{1}{2}}){\displaystyle \frac{c}{\nu }}$  (n=0,1,2,3...)
⟹ν=(n+12)3500.35=1000(n+12)=500Hz,1500Hz,2500Hz....$⟹\nu =(n+{\displaystyle \frac{1}{2}}){\displaystyle \frac{350}{0.35}}=1000(n+{\displaystyle \frac{1}{2}})=500Hz,1500Hz,2500Hz....$.

Definition

Constructive Interference

Constructive interference occurs when the phase difference between the waves is an even multiple of (180) (a multiple of 2, 360)etc.

Definition

Destructive Interference

Destructive interference occurs when the difference is an odd multiple of . ... At some points, these will be in phase, and will produce a maximum displacement

Definition

Equation of Standing Wave

Standing Waves:
A wave travelling along the +x direction is reflected at a fixed point. The result of its superposition is a standing wave.
y1(x,t)=Acos(kx−ωt)$y_1(x,t)=A\cos (kx-\omega t)$
y2(x,t)=−Acos(kx+ωt)$y_2(x,t)=-A\cos (kx+\omega t)$
y(x,t)=A[cos(kx−ωt)−cos(kx+ωt)]$y(x,t)=A[\cos (kx-\omega t)-\cos (kx+\omega t)]$
⟹y(x,t)=2Asin(kx)sin(ωt)$⟹y(x,t)=2A\sin (kx)\sin (\omega t)$
If kx=0,π,2π,...$kx=0,\pi ,2\pi ,...$
⟹x=0,λ/2,λ,3λ/2,...$⟹x=0,\lambda /2,\lambda ,3\lambda /2,...$
∴y(x,t)=0$\therefore y(x,t)=0$
So, no motion for these points (nodes).
If kx=π/2,3π/2,..$kx=\pi /2,3\pi /2,..$
⟹x=λ/4,3λ/4,...$⟹x=\lambda /4,3\lambda /4,...$
∴y(x,t)=±2Acos(ωt)$\therefore y(x,t)=\pm 2A\cos (\omega t)$
So, these points oscillate with the maximum possible amplitude (antinodes).

Definition

Hormonics and Overtone

An overtone is any frequency greater than the fundamental frequency of a sound. Using the model of Fourier analysis, the fundamental and the overtones together are called partials. Harmonics, or more precisely, harmonic partials, are partials whose frequencies are integer multiples of the fundamental (including the fundamental which is 1 time itself).

Definition

Define and find higher harmonics and overtones for standing wave in a string fixed at one end

 v=(n+12)v2L=n+122LF/μ−−−−√$v=(n+{\displaystyle \frac{1}{2}}){\displaystyle \frac{v}{2L}}={\displaystyle \frac{n+{\displaystyle \frac{1}{2}}}{2L}}\sqrt{F/\mu }$.

These are the normal frequencies of vibration. The fundamental frequency is obtained when n=0, ie,

v0=v/4L$v_0=v/4L$.

The overtone frequencies are

v1=3v4L=3v0$v_1=\frac{3v}{4L}=3v_0$,

v3=5v4L=5v0$v_3=\frac{5v}{4L}=5v_0$,

v3=7v4L=7v0$v_3=\frac{7v}{4L}=7v_0$, etc.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14  Page 15