IEMDaily - Video Lecture Notes

Definition

Wave Motion

Wave motion transfers energy from one point to another, which displace particles of the transmission medium, that is, with little or no associated mass transport. Waves consist, instead, of oscillations or vibrations (of a physical quantity), around almost fixed locations.

Definition

Propagation of energy in wave motion

Wave is an oscillation accompanied by a transfer of energy that travels through a medium. For example, it can be seen that the waves move radially outwards when a stone is dropped in water and hence transferring energy.

Formula

What is Wave?

A wave can be described as a disturbance that travels through a medium from one location to another location
Waves are of different kind such as waves on water, sound waves, light waves, radio waves etc.

Definition

Mechanical Waves

A mechanical wave is a wave that is an oscillation of matter, and therefore transfers energy through a medium. While waves can move over long distances, the movement of the medium of transmission of the material is limited. Therefore, oscillating material does not move far from its initial equilibrium position.

Definition

Medium of Propagation of Mechanical waves

Sound is a vibration that propagates as a typically audible mechanical wave of pressure and displacement, through a medium such as air or water.

Example

Combined transverse and longitudinal wave

Water waves are an example of waves that involve a combination of both longitudinal and transverse motions. All particles in such waves have two components of displacement, one in the direction of the motion of the wave and other in the direction perpendicular to the direction of the motion of the wave.

Definition

Crests and troughs

A crest is the point on a transverse wave with the maximum positive displacement within a cycle.
A trough is a point on a transverse wave with the minimum displacement ( maximum negative displacement ) in a cycle.

Example

Write the wave equation from given information about oscillating source

Example: Transverse waves on a string have wave speed 12.0 m/s, amplitude 0.05 m and wavelength 0.4 m. The waves travel in the + x direction and at t = 0 the x = 0 end of the string has zero displacement and is moving upwards.

Solution:
A wave travelling in +x direction is represented by

y = A \sin (ω t - k x)

where

ω = 2 π ν

and

k = \frac{2 π}{λ}

We know that speed of wave=

v = λ ν

Thus here

ω = 2 π \times \frac{v}{λ} = 2 π \times \frac{12}{0.4} = 60 π s^{- 1}

and

k = \frac{2 π}{0.4} = 5 π m^{- 1}

.
Thus wave is

y = (0.05) s i n (60 π t - 5 π x)

Definition

Amplitude of SHM

Amplitude is maximum displacement from the equilibrium position.
In SHM amplitude and displacement are related in the following way.

x = A s i n (w t)

Example

Find phase from equation of SHM and relate with starting position

Example: The equation of the displacement of two particles making SHM are represented by

y_{1}

= a sin

(ω t + ϕ)

y_{2}

= a cos

(ω t)

What is the phase difference of the velocities of the two particles?

Solution:

y_{1} = a s i n (ω t + ϕ)

y_{2} = a c o s (ω t)

y_{1} = a ω c o s (ω t + ϕ) = a ω s i n (ω t + ϕ +^{π} /_{2})

y_{2} = - a ω s i n (ω t) = a ω s i n (π + ω t)

therefore phase difference

= ω t + ϕ +^{π} /_{2} - (π + ω t)

= ϕ - π /_{2}

Definition

Amplitude of a travelling wave

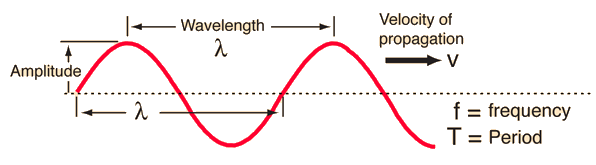
Amplitude is the distance from the rest position to the crest position which is half the vertical distance from a trough to a crest.

Definition

Phase of a travelling wave

Phase in sinusoidal functions or in waves has two different, but closely related, meanings. One is the initial angle of a sinusoidal function at its origin and is sometimes called phase offset or phase difference. Another usage is the fraction of the wave cycle that has elapsed relative to the origin.