Rotational Dynamics Concepts Page - 7

Definition

Areal velocity of a point object

Areal velocity is defined as the rate of change of area of segment subtended by the revolving body about its axis of rotation.
dA⃗ dt=r⃗ ×v⃗ 2${\displaystyle \frac{d\overrightarrow{A}}{dt}}={\displaystyle \frac{\overrightarrow{r}\times \overrightarrow{v}}{2}}$
dA⃗ dt=L⃗ 2m${\displaystyle \frac{d\overrightarrow{A}}{dt}}={\displaystyle \frac{\overrightarrow{L}}{2m}}$ for a point object

Definition

Conservation of Angular Momentum

Angular momentum is the rotational analog of linear momentum. It is an important quantity in physics because it is a conserved quantity the angular momentum of a system remains constant unless acted on by an external torque.

Example

Conservation of Angular Momentum

Torque is defined as τ=dLdt$\tau ={\displaystyle \frac{dL}{dt}}$
If τ=0$\tau =0$
then L⃗ $\overrightarrow{L}$ = constant

Essentially, it means in the absence on external torque angular momentum of the system of particles doesn't change.

Example

Relation between rate of change on angular momentum with net torque on a system of particles

For a system of particles rate of change of angular momentum is is equal to net torque acting on it.
 τ=ΔLΔt$\tau ={\displaystyle \frac{\mathrm{\Delta }L}{\mathrm{\Delta }t}}$

Example

Numerical to find moment of force (torque)

Example: The handle of a door is at a distance 40cm$40cm$ from axis of rotation. If a force 5N$5N$ is applied on the handle in a direction 30∘${30}^{\circ }$ with plane of door, then find the torque.

Example

Problem on fixed axis rotation with constant angular velocity

Example: A conical pendulum consists of a simple pendulum moving in a horizontal circle as shown. C is the pivot, O the centre of the circle in which the pendulum bob moves and ω$\omega$ is the constant angular velocity of the bob. If L⃗ $\overrightarrow{L}$ is the angular momentum about point C, then how its value will vary?
Solution: The direction of L$L$ is perpendicular to the line joining the bob to point C. Since this line keeps changing its orientation in space, direction of L$L$ keeps changing however as is constant, magnitude of L$L$ remain constant.
|v⃗ |=|(r⃗ ×ω⃗ )|=constant$\left|\overrightarrow{v}\right|=|(\overrightarrow{r}\times \overrightarrow{\omega })|=constant$ since ω$\omega$ is constant and the radius of the circle is constant.
The length of the line joining the C and the bob of the pendulum is constant.
Hence ∣∣∣r′→∣∣∣=constant$\left|\overrightarrow{r^{\prime }}\right|=constant$
∴∣∣L⃗ ∣∣=∣∣∣r′→×p⃗ ∣∣∣=constant$\therefore \left|\overrightarrow{L}\right|=|\overrightarrow{r^{\prime }}\times \overrightarrow{p}|=constant$
NB
: The torque about point is perpendicular to the angular momentum vector about point C. Hence it can only change the direction of L, and not its magnitude.

Example

Conservation of Angular Momentum

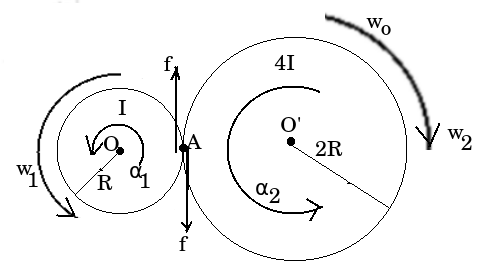
Example:
Two cylinders having radii 2R$2R$ and R$R$ and moment of inertia 4I$4I$
and I$I$ about their central axes are supported by axles perpendicular to their planes. The large cylinder is initially rotating clockwise with angular velocity ω0${\omega }_0$. The small cylinder is moved to the right until it touches the large cylinder and is caused to rotate by the frictional force between the two. Eventually slipping ceases and the two cylinders rotate at constant rates in opposite direction. During this how the angular momentum and kinetic energy will change?
Solution:
There is a finite net torque about point O, O' and A. Thus angular momentum is not conserved.Initial K.E,    Ei=12(4I)w2o=2Iw2o$E_i={\displaystyle \frac{1}{2}}(4I)w_o^2=2I{w}_o^2$
Final K.E,   Ef=12Iw2o+12(4I)w2o4=Iw2o$E_f={\displaystyle \frac{1}{2}}I{w}_o^2+{\displaystyle \frac{1}{2}}(4I){\displaystyle \frac{w_o^2}{4}}=I{w}_o^2$
Thus K.E is also not conserved.

Example

Application of conservation of angular momentum of a rigid body about a fixed axis

Example:
A diver jumps with an angular velocity ω$\omega$ and then curls his body to so that the moment of inertia is halved. What is the final angular velocity of the diver?
Solution:
Let initial moment of inertia be Ii$I_i$ and final angular velocity be ωf${\omega }_f$.
By conservation of angular momentum,
Iiω=Ii2ωf$I_i\omega ={\displaystyle \frac{I_i}{2}}{\omega }_f$
ωf=2ω

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12