IEMDaily - Video Lecture Notes

Example

Moment of inertia of a rectangular plate

Example: The mass of a rectangular plate of uniform thickness is

M

and its
length and breadth are

L

and

\frac{L}{2}

respectively. What is the
expression for moment of inertia of same plate about an axis
perpendicular to plane of plate and passing through one of four corners?

Solution:
Moment of inertia of rectangle

I = \frac{M (a^{2} + b^{2})}{12}

, now

b = L / 2

. So we get

I_{c m} = \frac{5 M L^{2}}{48}

Now distance of center from the corner is

d = \sqrt{(L / 2)^{2} + (L / 4)^{2}} = \frac{\sqrt{5} L}{4}

,So using parallel axis theorem

I = I_{c m} + M d^{2} = \frac{5 M L^{2}}{48} + \frac{M (5 L)}{16}

I = \frac{5 M L^{2}}{12}

Example

Masses attached to fixed pulleys with given moment of inertia

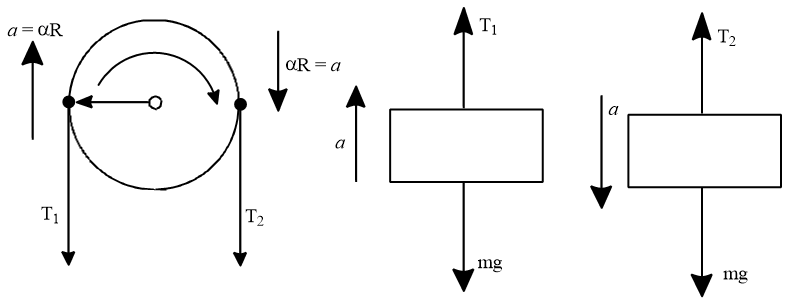
Example: Two blocks of masses

1

kg and

2

kg are suspended at the end of a light string passing over a frictionless pulley of mass

4

kg and radius

10

cm.
When the masses are released, what will the acceleration of the masses?

Solution: Refer to the diagram.
For the two blocks the equations of motion are:

T_{1} - m_{1} g = m_{1} a

......(1)

m_{2} g - T_{2} = m_{2} a

......(2)

For the pulley, equation of motion for rotation is( since the pulley only rotates)
net torque

τ_{n e t} = I α

∴ T_{2} R - T_{1} R = \frac{1}{2} M R^{2} α

....(3)
Dividing (3) by

R

and adding (1) and (2) to it we get,

m_{2} g - m_{1} g = m_{2} a + m_{1} a + \frac{M}{2} R α

∴ m_{2} g - m_{1} g = m_{2} a + m_{1} a + \frac{M}{2} a

\Rightarrow a = \frac{m_{2} - m_{1}}{m_{2} + m_{1} + \frac{M}{2}} g

.....(4)
Substituting

m_{1} = 1

m_{2} = 2

, and

M = 4

and

R = 10 c m = 0.1 m

in eqn(4), we get

a = \frac{2 - 1}{2 + 1 + \frac{4}{2}} g = \frac{g}{5}

Example

Masses attached to multiple fixed pulleys with defined moment of inertia

Example: In the arrangement shown in figure above, a weight

A

possesses mass

m

, a pulley

B

possesses mass

M

. Also known are the moment of inertia

I

of the pulley relative to its axis and the radii of the pulley

R

and

2 R

. The mass of the threads is negligible. If the acceleration of the weight

A

after the system is set free is

w = \frac{b (M + b m) g}{(M + 9 m + \frac{I}{R^{2}})}

, find the value of

b

.

Solution:Let us depict the forces acting on the pulley and weight

A

, and indicate positive direction for

x

and

φ

as shown in figure below. For the cylinder from the equation

F_{x} = m w_{c x}

and

N_{c z} = I_{c} β_{z}

, we get

M g + T_{A} - 2 T = M w_{c}

....(1)
and

2 T R + T_{A} (2 R) = I β = \frac{I w_{c}}{R}

.....(2)
For the weight

A

from the equation

F_{x} = m w_{x}

m g - T_{A} = m w_{A}

......(3)
As there is no slipping of the threads on the pulleys,

w_{A} = w_{c} + 2 β R = w_{c} + 2 w_{c} = 3 w_{c}

.....(4)
Simultaneous solutions of above four equations gives,

w_{A} = \frac{3 (M + 3 m) g}{(M + 9 m + \frac{I}{R^{2}})}

Definition

Clockwise and Anticlockwise Moments

Conventionally, if the effect on the body is to turn it anticlockwise, moment of force is called the anticlockwise moment and it is taken positive while if the effect on the body is to turn it clockwise, the moment of force is called the clockwise moment and it is taken negative.

Definition

Units of Moment of Force

1 N m = 10^{5} d y n e \times 10^{2} c m

= 10^{7} d y n e c m

1 k g f \times 1 m = 9.8 N m

1 g f \times 1 c m = 980 d y n e c m

Definition

Moment of Force or Torque

Torque or moment of force is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist to an object.