IEMDaily - Video Lecture Notes

Formula

Maximum Height of a Projectile

In vertically upward projection case

θ = 90^{0}

Therefore maximum height for an object projected vertically upwards is

\frac{v^{2}}{2 g}

Example: A particle is thrown vertically upwards with speed of 10 m/s. Find the maximum height reached by it. Also, find the time to reach maximum height.

Solution:

H = \frac{v^{2}}{2 g}

H = 10^{2} / 20 = 5 m

Time taken in reaching height:

t^{2} = 2 H / g

t^{2} = 2 \times 5 / 10

t = 1 s

Example

Equations of Motion under free fall

In free fall initial velocity of the particle is zero.
Therefore, equations of motion are:

v = g t .

h = \frac{g t^{2}}{2}

and

v^{2} = 2 g s

Example

Problem on two dimensional motion

Problem:
A particle starts from rest with initial velocity

\vec{v} = \hat{i} + \hat{j}

\frac{m}{s}

, and acceleration

\hat{a} = - 2 \hat{i} + \hat{j}

\frac{m}{s^{2}}

, find net displacement of particle after 4 sec.

Solution:
Given data -
Initial velocity =

\vec{v} = \hat{i} + \hat{j}

\frac{m}{s}

Acceleration =

\hat{a} = - 2 \hat{i} + \hat{j}

\frac{m}{s^{2}}

time = 4 sec
Hence
Displacement of particle becomes

\vec{r} = \vec{v} t + \frac{1}{2} \vec{a} t^{2}

= (\hat{i} + \hat{j}) + \frac{1}{2} (- 2 \hat{i} + \hat{j}) 4^{2}

= - 15 \hat{i} + 9 \hat{j}

Example

Problems on freely falling objects

Example: A stone projected vertically up from the top of a cliff reaches the foot of the cliff in

8 s

. If it is projected vertically downwards with the same speed, it reaches the foot of the cliff in

2 s

. Then what is its time of free fall from the cliff?

Solution:A to B

\overset{V I α C}{\to}

(with

u

)

\Rightarrow H = u (

) - \frac{1}{2} g (8)^{2} = 8 u - 32 g - (1)

A to B (with

u

downwards)

\Rightarrow H = u (2) - \frac{1}{2} g (2)^{2} = 2 u - 2 g - (2)

free fall,

e q^{n} (1) - e q^{n} (2)

t = \sqrt{\frac{2 H}{g}} \Rightarrow 6 u = 30 g

u = 5 g

So,

H = 10 g - 2 g = 8 g

(from 2)
hence,

t = \sqrt{\frac{2 \times 8 g}{g}} = 4 s e c .

Definition

Problems on motion under gravity including collisions with the ground

In free fall initial velocity of the particle is zero.
Therefore,

h = 1 / 2 g t^{2}

If a particle is falling from 19.6m then after how long the particle will collide the ground:

19.6 = 1 / 2 \times 9.8 \times t^{2}

t = 2 s

Definition

Projectile Motion

An object that is in flight after being thrown or projected is called a projectile and it's motion is called projectile motion. The motion of a projectile may be thought of as the result of two separate, simultaneously occurring components of motions. One component is along a horizontal direction without any accelaration and the other along the vertical direction with constant accelaration due to the force of gravity.

Parameters of projectile motion:
1. Horizontal Range of the projectile.
2. Maximum height of the projectile.
3. Time of flight of the projectile.

Example

Understanding displacement,velocity and acceleration vectors in projectile motion

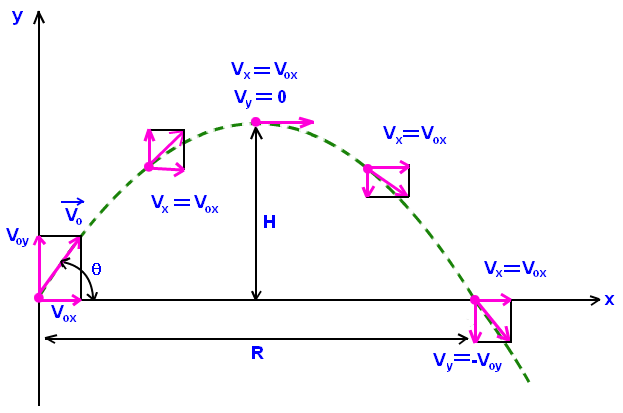
For a projectile motion displacement can be calculated from the point of projection along the direction of projection. Velocity has two components

v c o s θ

in horizontal and

v s i n θ

in vertical direction ,in which horizontal component of velocity remains constant because of absence of force. Acceleration due to gravity is present throughout the motion in vertical direction.

Formula

Derive formula for various parameters for projectile from certain height above the ground

Projectile is projected from height h at an angle of

θ

with velocity v.

The basic equations of kinematics at the landing point after flight time T are

0 = h + v_{y} T - \frac{1}{2} g T^{2}

..........(1)

vertically and

R = v_{x} T

..........(2)

horizontally. Substitute Eq. (2) for T into (1) and convert from rectangular to polar components to get

h (1 + c o s 2 θ) = \frac{g R^{2}}{v^{2}} - R s i n 2 θ

............(3)

Maximize R by differentiating this expression with respect to

θ

and putting

\frac{d R}{d θ} = 0

to obtain an expression for the optimum launch angle,

t a n (2 θ)

\frac{R}{h} ⟹ θ = \frac{1}{2} t a n^{- 1} \frac{R}{h}

..........(4)

This implies

c o s 2 θ = h (h^{2} + R^{2})^{- \frac{1}{2}}

and

s i n 2 θ = R (h^{2} + R^{2})^{- \frac{1}{2}} .

Substitute these equations in to eq. (3) to get max range,

h = \frac{g R^{2}}{2 v^{2}} - v^{2} 2 g ⟹ R = \sqrt{\frac{2 v^{2}}{g} (h + \frac{v^{2}}{2 g})}

..........(5)

Formula

projectile motion

Projectile motion with initial horizontal velocity:
When an object is thrown in the horizontal direction from a height, there is no force acting on a particle in horizontal, hence it is having constant velocity along the horizontal.
A gravitational force is acting downwards on the particle, hence it is accelerating downwards.
Hence, as a result path of projectile motion is parabolic.

Formula

Range of a Projectile Motion