IEMDaily - Video Lecture Notes

Example

Object crossing a river where relative velocity is inclined to river velocity

At a harbour, a boat is standing and wind is blowing at a speed of

\sqrt{2}

m/sec. due to which, the flag on the boat flutters along northeast. Now the boat enters in to river, which is flowing with a velocity of

2 m / s

due north. The boat starts with zero velocity relative to the river and its constant acceleration relative to the river is

0.2 m / s e c^{2}

due east. The direction in which the flag will flutter at

10

seconds is given by:

V_{w} = 1 \hat{i} + 1 \hat{j}

V = a t

V = (0.2) 10 = 2 m / s e c .

V_{b o a t} = 2 \hat{i} + 2 \hat{j}

V_{w / b o a t} = V_{w} - V_{b o a t}

V_{w / b o a t} = (1 \hat{i} + 1 \hat{j}) - (2 \hat{i} + 2 \hat{j}) = - 1 \hat{i} - 1 \hat{j}

So, the flag will flutter towards south-west.

Example

Problems on objects crossing a river to reach certain point on the opposite bank

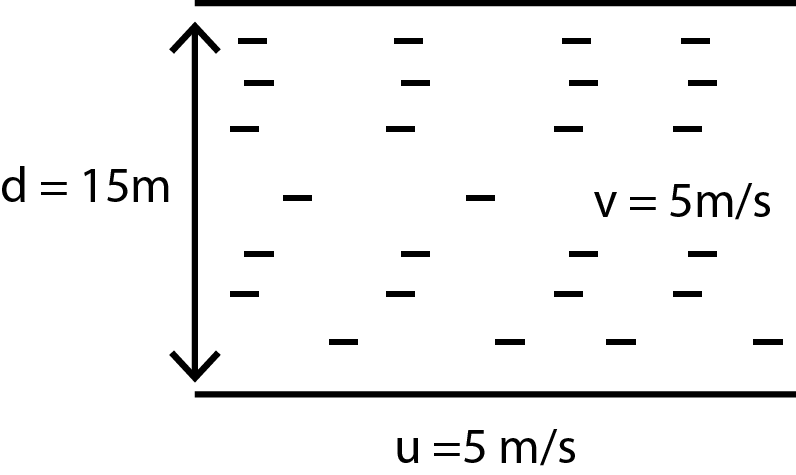
A man can swim in still water with a velocity

5 m / s

. He wants to reach at directly opposite point on the other bank of a river which is flowing at a rate of

4 m / s

. River is

15 m

wide and the man can run with twice the velocity as compared with velocity of swimming. If he swims perpendicular to river flow and then run along the bank, then time taken by him to reach the opposite point will be given by:

Time taken in crossing the river

T_{1} = \frac{d}{V_{m r}}

T_{1} = \frac{15}{5}, T_{1} = 3 s e c

Distance travel in this time along the river

D = V_{R} \times T_{1}

D = 4 \times 3, D = 12

T_{2} = \frac{D}{2 V_{m r}}, T_{2} = 1.2 s e c

T = T_{1} + T_{2}, T = 4.2 s e c

Example

Problem Analogous to Objects moving upstream or downstream in a river

Example:A man can row a boat with

4

km/h in still water. If he is crossing a river where the current is

2

km/h. Width of river is

4

km.How long will it take him to row

2

km up the stream and then back to his starting point?Solution:
Given :

V_{M W} = 4

km/hr

V_{R} = 2

km/hr
Distance covered in upstream or downward motion

d = 2

km each
For upstream motion of the boat :
Velocity of the man

V_{M} = V_{M W} - V_{W} = 4 - 2 = 2

km/h

∴

Time taken to go upstream

t_{1} = \frac{2}{2} = 1

hr

For downward motion of the boat or (return journey) :
Velocity of the man

V_{M} = V_{M W} + V_{W} = 4 + 2 = 6

km/h

∴

Time taken to go downstream

t_{2} = \frac{2}{6} = \frac{1}{3}

∴

Total time taken

T = t_{1} + t_{2} = 1 + \frac{1}{3} = \frac{4}{3}

hrs

Example

Relative motion in river crossing like situations

River-crossing scenarios are when a boat moves from one bank to another to cross a river flowing with a given velocity. An analogous scenario is discussed below.
A man can walk at a speed of

2

m/s. He walks in north direction on a platform of width

12

m moving east at a speed of

3

m/s. Find the displacement of the man relative to the platform along the direction of the motion of platform.

v_{m} = 2 \hat{j}

v_{p} = 3 \hat{i}

v_{m, p} = 2 \hat{j} - 3 \hat{i}

s_{m, p} = 2 t \hat{j} - 3 t \hat{i}

But,

s_{m, p} = s_{p} \hat{i} + 12 \hat{j}

From above two equations,

s_{p} = - 18 m

Example

Rain-Man Problem

A man runs with a velocity of

8 k m / h

towards east. The velocity of rainfall is

4 k m / h

vertically downwards. The angle at which the man should hold the umbrella so as to protect himself from the rain:

r =

rain

, g =

ground

& m =

man .We have,

\vec{v_{r m}} = \vec{v_{r g}} + \vec{v_{m g}}

Resultant

\vec{v_{r m}}

makes an angle of

θ = \tan^{- 1} \frac{8}{4} = {63.43}^{o}

with vertical So, man should rotates his umbrella in anticlockwise direction such that its makes an angle of

{63.43}^{o}

with vertical.

Example

Rain-Man Problem where rainfall is inclined to man's velocity

A man wearing a hat of extended length

12 c m

is running in rain falling vertically downwards with speed

10 m / s

. The maximum speed with which man can run, so that rain drops do not fall on his face (the length of his face below the extended part of the hat is

16 c m

)

V_{r a i n} = 10 m / s

(in negative

y

direction)
Let, velocity of man =

v

Also from the above diagram we get the value of

θ

t a n θ = \frac{16}{12} = \frac{4}{3}

then, velocity of rain w.r.t man

V_{r a i n / m a n}

v

(opposite to man i.e. in negative

x

direction)
For the required condition :

t a n θ = \frac{10}{v} = \frac{4}{3}

v = \frac{10 \times 3}{4} = 7.5 m / s

Definition

Velocity of approach and separation

Velocity of approach or separation is defined as the rate of change of relative displacement between two bodies (i.e. how fast a body approaches another body). Velocity of approach is defined when the displacement between the bodies is decreasing and separation when the displacement between the bodies is increasing.
Example:
When two bodies approach each other with different uniform speeds, the distance between them decreases by

120 m

per every

1 m i n

. Then, the velocity of approach is

120 m / m i n = 2 m / s

Example

Distance of closest approach

Example:
Two ships A and B are 10 km apart on a line running south to north. Ship A farther north is streaming west at 20 km/h and ship B is streaming north at 20 km/h. What is their distance of closest approach and how long do they to reach it?
Solution:
Ships A and B are moving with same speed 20 km/h in the directions shown in figure. It is two dimensional, two body problem with zero acceleration.
Let us find

{\vec{v}}_{B A}

{\vec{v}}_{B A} = {\vec{v}}_{B} - {\vec{v}}_{A}

Here,

| {\vec{v}}_{B A} | = \sqrt{{(20)}^{2} + {(20)}^{2}} = 20 \sqrt{2} k m / h

i.e.,

{\vec{v}}_{B A} i s 20 \sqrt{2}

km/h at an angle of

45^{\circ}

from east towards north. Thus, the given problem can be simplified as:
A is at rest and B is moving with

{\vec{v}}_{B A}

in the direction shown in figure.
Therefore, the minimum distance between the two is

s_{m i n} = A C = A B \sin 45^{\circ}

= 10 (\frac{1}{\sqrt{2}}) k m

= 5 \sqrt{2} k m

And the desired time is:

t = \frac{B C}{| {\vec{v}}_{B A} |} = \frac{5 \sqrt{2}}{20 \sqrt{2}} (B C = A C = 5 \sqrt{2} k m)

= \frac{1}{4} h

= 15 m i n

Definition

Heavy and light objects falls together on the earth surface

When a rubber ball and a metal ball of same size but different mass are thrown from a top of building at the same instant of time, both will come to fall on the ground at the same time when no other force will be acting on them, because earth pull both the objects with the same force.But a feather and a stone dropped from same height will not fall on the ground at the same time as the feather will be easily driven away by the moving wind/air.

Definition

Interpret conclusions by observing graphs