Current Electricity Concept Page - 6

Example

Resistors in series and parallel

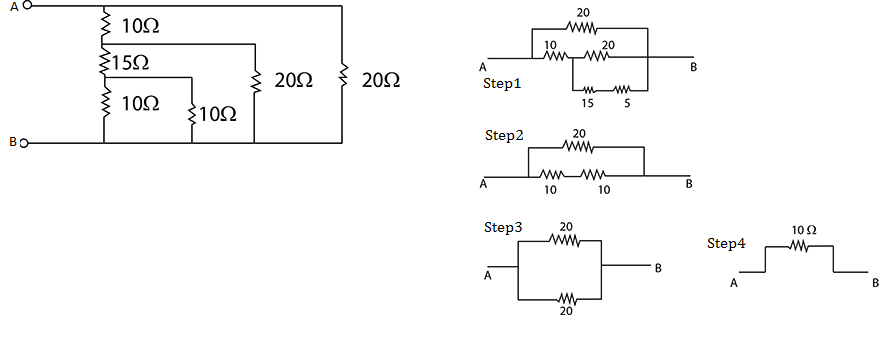
The effective resistance between A and B is:The circuit can be reduced as shown in the figure to obtain the equivalent resistance.
In step 1   The innermost rectangle has two  10Ω$10\mathrm{\Omega }$ resistances in parallel. 5 Ω$\mathrm{\Omega }$ equivalent resistance is kept in place of both.

Step 2. In step one 15 Ω$\mathrm{\Omega }$ and 5 Ω$\mathrm{\Omega }$ are in series which combined are in parallel to 20 Ω$\mathrm{\Omega }$. The equivalent resistance of 10 Ω$\mathrm{\Omega }$ is kept in the place of them.

Step 3. In step 2 now two 10 Ω$\mathrm{\Omega }$ are in series. The equivalent resistance of 20$20$ Ω$\mathrm{\Omega }$ is kept.

Step 4. In step 3 two 20$20$ Ω$\mathrm{\Omega }$ resistance are in parallel, which give equivalent resistance between A and B as 10$10$ Ω$\mathrm{\Omega }$.

Example

Multiple resistors in series and parallel

In the circuit given below all resistances are of values 5$5$ ohm each. The currents i1$i_1$and i2$i_2$ given that the e.m.f. of the cell is 11 V$11V$ are:Req=5+15×520+5$R_{eq}=5+{\displaystyle \frac{15\times 5}{20}}+5$
         =554$={\displaystyle \frac{55}{4}}$

I×Req=V$I\times R_{eq}=V$   
 
I=11554=45A$I={\displaystyle \frac{11}{{\displaystyle \frac{55}{4}}}}={\displaystyle \frac{4}{5}}A$

I1=I×1520=45×34=0.6A$I_1=I\times {\displaystyle \frac{15}{20}}={\displaystyle \frac{4}{5}}\times {\displaystyle \frac{3}{4}}=0.6A$

I2=I×520=45×14=0.2A$I_2=I\times {\displaystyle \frac{5}{20}}={\displaystyle \frac{4}{5}}\times {\displaystyle \frac{1}{4}}=0.2A$

Example

Electrical resistance circuits using symmetry

Twelve resistances, each of resistance R$R$ are connected in the circuit as shown in the figure. Net resistance between points A$A$ and C$C$ would be:By symmetric rule, RBG$R_{BG}$  and  RED$R_{ED}$ can be removed.
[∵$\because$  no current flows through them]
Then the circuit becomes as shown.
⇒1RAC=12R+12R+13R$\Rightarrow {\displaystyle \frac{1}{R_{AC}}}={\displaystyle \frac{1}{2R}}+{\displaystyle \frac{1}{2R}}+{\displaystyle \frac{1}{3R}}$
 =1R+13R$={\displaystyle \frac{1}{R}}+{\displaystyle \frac{1}{3R}}$
⇒RAC=3R4$\Rightarrow R_{AC}={\displaystyle \frac{3R}{4}}$

Shortcut

Procedure to solve Infinite circuits

Let the infinite circuit be as shown in figure (a). Here are the steps to solve it.

1. Assume the equivalent resistance of the system in the dotted box be Req$R_{eq}$. 
2. Then calculate the equivalent resistance of the whole system taking Req$R_{eq}$ in parallel with the remaining system as shown in figure (b).
3. Now this final calculated value is also Req$R_{eq}$ (∵$\because$ the part of infinity is also infinity).

Example

Electrical resistance using star-delta rule

The resistance of all the wires between any two adjacent dots is R$R$. The equivalent resistance between A$A$ and B$B$ as shown in Figure is:
Here the equivalent resistance of each triangle is Req1=(R+R)R(R+R)+R=(2/3)R$R_{eq1}={\displaystyle \frac{(R+R)R}{(R+R)+R}}=(2/3)R$
Now reduce the side by connecting resistance in series as shown in figure.
here, Req2=(2/3)R+(2/3)R=(4/3)R$R_{eq2}=(2/3)R+(2/3)R=(4/3)R$.

Now the circuit is a balanced Wheatstone bridge . So middle resistor R is not working.
Thus, RAB=[(4/3)R+R][(4/3)R+R][(4/3)R+R]+[(4/3)R+R]=(7/6)R$R_{AB}={\displaystyle \frac{[(4/3)R+R][(4/3)R+R]}{[(4/3)R+R]+[(4/3)R+R]}}=(7/6)R$ 

Diagram

Positive and negative terminals of an electric cell

Every cell has a positive and a negative terminal and based on their polarity it is connected in the electrical circuit.
For example in a circuit positive terminal of a cell is always connected to a negative terminal of the other cell, otherwise the current will not flow in the circuit as the polarity become same on both the side and no potential difference will be there.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10  Page 11
Page 12  Page 13  Page 14  Page 15  Page 16