Nuclear Physics Concept Page - 4

Definition

Continuous Spectrum

1. A continuous spectrum : A spectrum having no apparent breaks or gaps throughout its wavelength range is termed as continuous spectrum. It is produced by hot solid, liquid, or very dense gas.

Definition

Spectral series

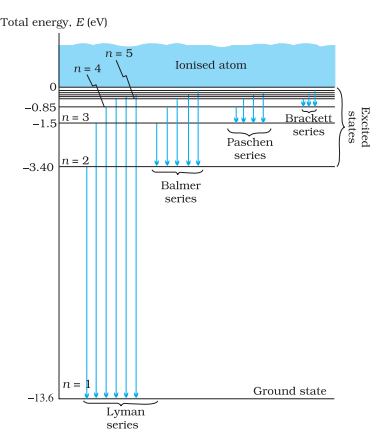
The emission spectrum of atomic hydrogen is divided into a number of spectral series, with wavelengths given by the Rydberg formula. These observed spectral lines are due to the electron making transitions between two energy levels in the atom.
Rydberg formula:
1λ=RZ2(1n′2−1n2)${\displaystyle \frac{1}{\lambda }}=R{Z}^2({\displaystyle \frac{1}{{n^{\prime }}^2}}-{\displaystyle \frac{1}{n^2}})$
where Z=1 for hydrogen atom.

Definition

Bohr's model

The Bohr model depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus similar in structure to the solar system, but with attraction provided by electrostatic forces rather than gravity.

1. Bohr's first postulate was that an electron in an atom could revolve in certain stable orbits without the emission of radiant energy, contrary to the predictions of electromagnetic theory. According to this postulate, each atom has certain definite stable states in which it can exist, and each possible state has definite total energy. These are called the stationary states of the atom.
2. Bohrs second postulate defines these stable orbits. This postulate states that the electron revolves around the nucleus only in those orbits for which the angular momentum is some integral multiple of h/2 where h is the Plancks constant (=6.6×1034Js$=6.6\times {10}^{34}Js$). Thus the angular  momentum (L) of the orbiting electron is quantised. That is
   L=nh2π$L={\displaystyle \frac{nh}{2\pi }}$
3. Bohrs third postulate incorporated into atomic theory the early quantum concepts that had been developed by Planck and Einstein.It states that an electron might make a transition from one of its specified non-radiating orbits to another of lower energy. When it does so, a photon is emitted having energy equal to the energy difference between the initial and final states. The frequency of the emitted photon is then given by
   hν=Ei−Ef$h\nu =E_i-E_f$

Definition

Bohr radius

The Bohr radius (a0$a_0$) is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state.
a0=h2ϵ0πme2=5.29×10−11m$a_0={\displaystyle \frac{h^2{ϵ}_0}{\pi m{e}^2}}=5.29\times {10}^{-11}m$

Definition

Accelerated atomic electron spiral into nucleus

The model of the atom proposed by Rutherford assumes that the atom,  consisting of a central nucleus and revolving electron is stable.object which  moves in a circle is being constantly accelerated the acceleration being centripetal in nature. According to classical electromagnetic theory, an accelerating charged particle emits radiation in the form of electromagnetic waves. The energy of an accelerating electron should therefore, continuously decrease. The electron would spiral inward and eventually fall into the nucleus . Thus, such an atom can not be stable. As the electrons spiral inwards, their angular velocities and hence their frequencies would change continuously, and so will the frequency of the light emitted. Thus, they would emit a continuous spectrum, in contradiction to the line spectrum actually observed.

Formula

Electron orbits

According to Rutherford's nuclear model, the nucleus is at the center and electrons revolve in a circular orbit. 
There must be a centripital force on the electron which enables it to move in a circular orbit.
Hence,
mv2r=k(ze)(e)r2${\displaystyle \frac{m{v}^2}{r}}={\displaystyle \frac{k(ze)(e)}{r^2}}$
where, ze: charge on nucleus, e: charge on electron, r: orbital radius
Also k=4πe0$k=4\pi e_0$
Hence solving this equation we get,
r=e24πe0mv2$r={\displaystyle \frac{e^2}{4\pi e_{0}m{v}^2}}$
 

Definition

Orbital radius and electron velocity

The electrostatic force of attraction,Fe$F_e$ between the revolving electrons and the nucleus provides the requisite centripetal force (Fc$F_c$) to keep them in their orbits. Thus, for a dynamically stable orbit in a hydrogen atom
Fe=Fc$F_e=F_c$
mv2r=14πϵ0e2r2${\displaystyle \frac{m{v}^2}{r}}={\displaystyle \frac{1}{4\pi {ϵ}_0}}{\displaystyle \frac{e^2}{r^2}}$
Thus the relation between the orbit radius and the electron velocity is
r=e24πϵ0mv2$r={\displaystyle \frac{e^2}{4\pi {ϵ}_{0}m{v}^2}}$

Definition

Quantum number of orbit

A 10 kg satellite circles earth once every 2 h in an orbit having a radius of 8000 km. Assuming that Bohrs angular momentum postulate applies to satellites just as it does to an electron in the hydrogen atom, find the quantum number of the orbit of the satellite.
Solution:
We have mvnrn=nh2π$m{v}_n{r}_n={\displaystyle \frac{nh}{2\pi }}$
Given m=10kg, rn=8×106$r_n=8\times {10}^6$, T=7200s
vn=2πrnT$v_n={\displaystyle \frac{2\pi r_n}{T}}$
The quantum number of the orbit of satellite
n=(2πrn)2×m(T×h)=(2π8×106)2×10(7200×h)=5.3×1045$n=(2\pi r_n{)}^2\times {\displaystyle \frac{m}{(T\times h)}}=(2\pi 8\times {10}^6{)}^2\times {\displaystyle \frac{10}{(7200\times h)}}=5.3\times {10}^{45}$

Definition

Electron distribution in orbit or shells

According to atomic models, electrons move around the nucleus of atom in electron shells. Electrons in different shells have different energies. Each shell is represented by a number, ′n′${}^{\prime }{n}^{\prime }$, which is known as a shell number or energy level index.
The shell closest to the nucleus (and has the lowest energy) is called the K$K$-shell (n=1)$(n=1)$, the shell farther away (and has higher energy than K-shell) is called the L$L$-shell (n=2)$(n=2)$, in the similar way there is M$M$ shell (n=3)$(n=3)$ and N$N$ shell (n=4)$(n=4)$.Bohr and Bury proposed the following rules for electron distribution.
Rule 1: The maximum number of electrons present in a shell is given by the formula 2n2$2n^2$, where 'n' is the shell number.
Rule 2: Each energy level or electron shell is further divided into sub shells. The maximum number of electrons that can be accommodated in each sub shell is 8.
Rule 3: Electrons cannot be filled in a given shell unless the inner shells are completely filled i.e., shells are filled in step wise manner.

Formula

Dependence of velocity, radius and energy on orbit of electron

Using Bohr's postulate, we can derive the expressions for radius(rn$r_n$), velocity(vn$v_n$), momentum and energy (En)$(E_n)$ of an electron revolving in an orbit n$n$. We generally need to memorize the dependency of these variables on the orbit, n and atomic number, Z of the electron.
Let us see these dependencies.

• vn∝Zn$v_n\propto {\displaystyle \frac{Z}{n}}$
• rn∝n2Z$r_n\propto {\displaystyle \frac{n^2}{Z}}$
• En∝Z2n2$E_n\propto {\displaystyle \frac{Z^2}{n^2}}$

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10  Page 11
Page 12  Page 13  Page 14