Fluid Mechanics Concept Page - 5

Example

Inferring pressure at a point from density of streamlines

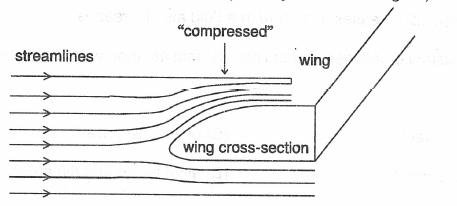
Example: Consider an airplane moving through the air at velocity v=200m/s$v=200m/s$. The streamlines which move just over the top are compressed to eight-tenths their normal area and given that those under the wing are not compressed at all (Density of air 1.3kg/m3$1.3kg/m^3$). What is the difference in the pressure between the air just over the wing P1${\mathrm{P}}_1$ and that under the wing P2${\mathrm{P}}_2$ ?

Solution:Compression of the streamlines means that the stream tube above the wing
has a smaller cross-sectional area than that in front of the plane and from the continuity equation , the velocity v′$v^{\prime }$ of the air must, therefore, be greater above the wing. Area A′=810A$A^{\prime }={\displaystyle \frac{8}{10}}A$ ⇒AA′=108$\Rightarrow {\displaystyle \frac{A}{A^{\prime }}}={\displaystyle \frac{10}{8}}$
From continuity equation,
Av=A′v′$Av=A^{\prime }{v}^{\prime }$
∴v′=AA′v=108×200=250ms−1$\therefore v^{\prime }={\displaystyle \frac{A}{A^{\prime }}}v={\displaystyle \frac{10}{8}}\times 200=250m{s}^{-1}$
The greater velocity (v′$v^{\prime }$,as obtained above) implies lower pressure than the normal pressure of the air in front of the plane. Given that the flow-lines under the wing are not compressed at all.
The pressure under the wing is just the normal pressure of the air in front of the wing.
From Bernoulli's equation , with both points 1 (for P1$P_1$) and 2 (for P2$P_2$) at effectively same elevation.
Pa+12ρav21=Pb+12ρbv22$P_a+{\displaystyle \frac{1}{2}}{\rho }_a{v}_1^2=P_b+{\displaystyle \frac{1}{2}}{\rho }_b{v}_2^2$
Given:
v2=200ms−1$v_2=200m{s}^{-1}$
∴P2−P1=12ρa(v21−v22)=12×1.3(2502−2002)=1.46×104Pa$\therefore P_2-P_1={\displaystyle \frac{1}{2}}{\rho }_a(v_1^2-v_2^2)={\displaystyle \frac{1}{2}}\times 1.3({250}^2-{200}^2)=1.46\times {10}^{4}Pa$

Definition

Direction of force on a surface in a static fluid

Force inside the static fluid acts perpendicular to the surfaces of fluid column. The direction of force on the top and bottom of a liquid column in a fluid column is shown in the attached figure as F1$F_1$ and F2$F_2$.

Example

Problem on U-tube containing immisible liquids

Example: The relative density of the liquid at the bottom of the U-tube is 11. 
Water is filled over it as shown. What is the difference in the liquid level in 
the U-tube?

Solution: By Pascal's law of pressure at equal level of fluid will have same value.
P1+ρWg(h0+Δh)=P2+ρWgh0+ρlgΔh$P_1+{\rho }_{W}g(h_0+\mathrm{\Delta }h)=P_2+{\rho }_{W}g{h}_0+{\rho }_{l}g\mathrm{\Delta }h$
(P1−P2)=(ρl+ρW)gΔh$(P_1-P_2)=({\rho }_l+{\rho }_W)g\mathrm{\Delta }h$
104=(11×103−103)(10)Δh⇒Δh=10cm${10}^4=(11\times {10}^3-{10}^3)\left(10\right)\mathrm{\Delta }h\Rightarrow \mathrm{\Delta }h=10cm$

Example

Force balance equation in static fluids

Example:
If the acceleration due to gravity is gms−2$gm{s}^{-2}$, a sphere of lead of density δ kg/m3$\delta kg/m^3$ is gently released in a column of liquid of density  dkg/m3(δ>d)$dkg/m^3(\delta >d)$, the sphere will fall vertically with what acceleration?
Solution:Force due to gravity =Vgρ$=Vg\rho$ 
Where V$V$ is the Volume of the Sphere , ρ$\rho$ is the density of the sphere and g$g$ is the acceleration due to gravity . 
Force due to buoyancy =Vgd$=Vgd$ where d$d$ is the density of the liquid . 
Net Force =Vg(ρ−d)$=Vg(\rho -d)$ 
∴$\therefore$ Net acceleration =Vg(ρ−d)Vρ=g(1−dρ)$={\displaystyle \frac{Vg(\rho -d)}{V\rho }}=g(1-{\displaystyle \frac{d}{\rho }})$

Example

Hollow sphere immersed in liquids

Example: A hollow sphere of mass M$M$ and radius r$r$ is immersed in a tank of water (density ρw${\rho }_w$). The sphere would float if it were set free. The sphere is tied to the bottom of the tank by two wires which makes angle 45∘${45}^{\circ }$ with the horizontal as shown in the figure. Find the tension T1$T_1$ in the wires?

Solution:When the sphere is tied to the strings, it is in equilibrium. net force 
on sphere is zero. i.e. net upward force= net downward force 
⇒W=2T1cos45∘+Mg$\Rightarrow W=2T_1\cos {45}^{\circ }+Mg$;    here Fb$F_b$ is the buoyant force
⇒43πR3ρwg=2T1cos45∘+Mg$\Rightarrow \frac{4}{3}\pi R^3{\rho }_{w}g=2T_1\cos {45}^{\circ }+Mg$
⇒T1=43πR3ρwg−Mg2√$\Rightarrow T_1={\displaystyle \frac{\frac{4}{3}\pi R^3{\rho }_{w}g-Mg}{\sqrt{2}}}$

Example

Objects immersed in multiple Immiscible static fluids

Example: A container of a large uniform cross-sectional area A$A$ resting on horizontal surface holds two immiscible,non-viscous and incompressible liquids of densities d$d$ and 2d,$2d,$ each of height H2${\displaystyle \frac{H}{2}}$  as shown in the figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H/2),$L(L<H/2),$ cross-sectional area A5${\displaystyle \frac{A}{5}}$ is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L4${\displaystyle \frac{L}{4}}$ in the denser liquid. Find force balance equation on the object.
The total pressure at the bottom of the container is given as =(xH+L4)dg+P0$=\left({\displaystyle \frac{xH+L}{4}}\right)dg+P_0$. Find x$x$ (atmospheric pressure =P0)$=P_0)$

Solution:
Total pressure at the bottom of cylinder is

P=weight of liquids+weight of cylinderA+P0$P={\displaystyle \frac{\text{weight of liquids+weight of cylinder}}{A}}+P_0$
P=[Ad(H2)g+A2d(H2)g]+A5(54d)LgA+P0$P={\displaystyle \frac{[Ad\left({\displaystyle \frac{H}{2}}\right)g+A2d\left({\displaystyle \frac{H}{2}}\right)g]+{\displaystyle \frac{A}{5}}\left({\displaystyle \frac{5}{4}}d\right)Lg}{A}}+P_0$

P=(6H+L4)dg+P0$P=\left({\displaystyle \frac{6H+L}{4}}\right)dg+P_0$

Here we are asked to find the total pressure at the bottom of the container and
not only the hydrostatic pressure; hence, we need to consider the total weight of the liquid and cylinder in the container.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14  Page 15  Page 16  Page 17  Page 18