Fluid Mechanics Concept Page - 3

Definition

Gauge and barometric Pressure

Gauge pressure is the amount by which the pressure measured in a fluid exceeds that of the atmospheric pressure.
pg=p−po$p_g=p-p_o$
where pg$p_g$ is absolute pressure or gauge pressure and po$p_o$ is atmospheric pressure.
Barometric pressure (also known as atmospheric pressure) is the force exerted by the atmosphere at a given point. It is known as the "weight of the air". A barometer measures barometric pressure. Measurement of barometric pressure can be expressed in millibars(mbar) or in inches or millimeters of mercury (Hg$Hg$).

Barometric pressure is measured by the height of mercury column.
p=hρg$p=h\rho g$

Example

Principle of Manometer and Example

A manometer is an instrument that uses a column of liquid to measure pressure

Example: The reading of a manometer fitted to a closed tap is 3.5 x 105${}^5$
Nm2${}^2$. If the valve is opened the reading of the manometer falls to
3 x 105${}^5$ Nm2${}^2$. What is the velocity of water?

Solution:
Applying bernouillis theorem to the fluid before and after the volume is opened,
p1+12fv21=p2+12fv22wherev1=0$p_1+{\displaystyle \frac{1}{2}}f{v}_1^2=p_2+\frac{1}{2}f{v}_2^{2}where{v}_1=0$
v1=0$v_1=0$
⇒3.5×105=3.0×105+12fv22$\Rightarrow 3.5\times {10}^5=3.0\times {10}^5+\frac{1}{2}f{v}_2^2$
2×0.5×105103=v2${\displaystyle \frac{2\times 0.5\times {10}^5}{{10}^3}}=v^2$
⇒v2=100m2/s2$\Rightarrow v^2=100m^2/s^2$
⇒v=10 m/s$\Rightarrow v=10m/s$

Definition

Units of density

Some common units of density are listed below:

• SI unit: kg/m3$kg/m^3$
• CGS unit: g/cm3$g/{cm}^3$.

Note: 1 kg/m3=10−3 g/cm3$1kg/m^3={10}^{-3}g/{cm}^3$

Definition

Relative Density definition

Relative density is defined as the ratio of density of a substance to the density of the standard substance. Usually water at 4o C$4^{o}C$ is used as a standard for a liquid or solid and air for a gas. It is a unitless quantity.

Definition

Relative Density

Density of water at 4o C$4^{o}C$ is given by ρw=1 g/cm3${\rho }_w=1g/{cm}^3$
Relative density, R.D.=ρ/ρw$R.D.=\rho /{\rho }_w$
                                   =ρ$=\rho$  (in CGS units)

Definition

Uses of relative density

Following are the uses of relative density:
1) It is used for determining the density of unknown substance from the known density of another substance.
2) It is used by geologist to find out the mineral content into the rock.
3) Testing purity of a substance (example gold).

Definition

Define and explain hydrostatic paradox

The barometric formula depends only on the height of the fluid chamber, and not on its width or length. Given a large enough height, any pressure may be attained. This feature of hydrostatics has been called the hydrostatic paradox. As expressed by W. H. Besant, "Any quantity of liquid, however small, may be made to support any weight, however large."

The hydrostatic paradox is explained by the fact that, since the hydrostatic pressure is always normal to a vessels walls, the force of the pressure on the inclined walls has a vertical component that compensates for the excess weight of the volume of fluid in a vessel that is wider at the top than a cylindrical vessel with the same bottom area and compensates for the lack of weight of the volume of fluid in a vessel that is narrower at the top.

Result

Hydraulic press

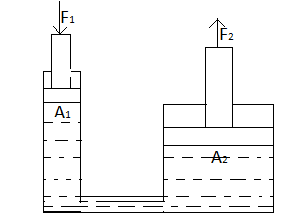
The hydraulic press works on the principle of Pascal's law. The pressure throughout a closed system is constant since there is no leakage. One part of the system is a piston acting as a pump, with a modest mechanical force acting on a small cross-sectional area, the other part is a piston with a larger area which generates a correspondingly large mechanical force. The larger force is used to press cotton or any other similar material against a fixed roof.

Result

Hydraulic jack

The hydraulic jack works on Pascal's law. An effort is applied on the piston of the jack with smaller area. This results in a greater force on the other end of the jack and hence results in a multiplication of force. 
In the given diagram,
F1A1=F2A2${\displaystyle \frac{F_1}{A_1}}={\displaystyle \frac{F_2}{A_2}}$
Since, A2>A1$A_2>A_1$
           F2>F1$F_2>F_1$

Result

Hydraulic brake

The hydraulic brake works on the principle of transmission of pressure by Pascal's Law. When the brake is pressed by applying a force F1$F_1$ the pressure in the braking fluid is increased. This is transmitted to the pistons with larger area which press against the break shoes (F2$F_2$) and the friction between the shoes and the rotor causes a braking torque to be generated, slowing the vehicle.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14  Page 15  Page 16  Page 17  Page 18