Fluid Mechanics Concept Page - 11

Definition

Principle and Working of Filter Pump

In Filter Pump, water from a tap flows at high speed out of the jet of water(nozzle). According to Bernoulli's Principle , the pressure of the moving air decreases as the speed of the air increases. The higher air pressure in the vessel pumps air from the side tube to which the vessel is connected.

Example

Wind Storms and Cyclones

Have you ever wondered why the roofs of houses get blown off during high winds?
High speed wind reduces the pressure above the roof while pressure below the roof is high, pushing it upwards hence roof gets blown off.
The damage done is directly proportional to speed to wind.
When high speed wind like cyclones hit out then we have seen an entire trees or big structure getting fall, so this is due to speed of wind blowing.
High speed wind are called cyclones which have huge capacity to blow big structures.

Definition

Working of bunsen burner on the bernoulli's principle

When a bunsen burner is connected to a gas supply, the gas flows at high velocity through a narrow passage in the burner. This creates a region of low pressure.
The outside air is at atmospheric pressure. Outside air flows in due to the pressure drop.
The mixture of gas and air enables the gas to burn completely to produce a clean, hot fire.

Example

Calculate of Velocity of efflux using Bernoulli's equation

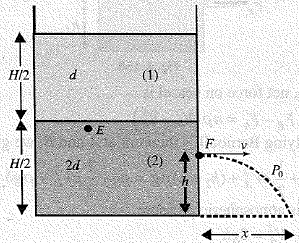
Example: A container of large uniform cross-sectional area A,$A,$ resting on
horizontal surface, holds two immiscible non-viscous and incompressible
liquids of density d$d$ and 2d,$2d,$ each of height H2${\displaystyle \frac{H}{2}}$ as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0$P_0$. A tiny hole of area s(s<<A)$s(s<<A)$ is punched on the vertical side of the container at a height h(h<H/2).$h(h<H/2).$ The initial speed of efflux of the liquid at the hole is given as v={(xH−4h)2g}−−−−−−−−−√$v=\sqrt{\left\{\frac{(xH-4h)}{2}g\right\}}$. Find x$x$.

Solution:Applying Bernoulli's theorm at points E($E($a point on the interface of
the liquids and on the top surface of the liquid of density 2d)$2d)$ and
F,$F,$
i.e., pressure energy +  kinetic energy + potential energy=constant$,\text{pressure energy + kinetic energy + potential energy}=\text{constant}$
⇒P0+H2dg+12(2d)×0+H22dg$\Rightarrow P_0+{\displaystyle \frac{H}{2}}dg+{\displaystyle \frac{1}{2}}(2d)\times 0+{\displaystyle \frac{H}{2}}2dg$
=P0+12(2d)v2+2hdg$=P_0+{\displaystyle \frac{1}{2}}(2d)v^2+2hdg$
⇒32Hdg=dv2+2hdg$\Rightarrow {\displaystyle \frac{3}{2}}Hdg=d{v}^2+2hdg$
⇒v2=32Hg−2hg=(3H−4h)2g$\Rightarrow v^2=\frac{3}{2}Hg-2hg={\displaystyle \frac{(3H-4h)}{2}}g$
∴v={(3H−4h)2g}−−−−−−−−−−−−−√$\therefore v=\sqrt{\left\{{\displaystyle \frac{(3H-4h)}{2}}g\right\}}$

Law

Torricelli's Law and Application

Torricelli's law is a theorem in fluid dynamics relating the speed of fluid flowing out of an opening to the height of fluid above the opening.

Example:
An enclosed tank containing a liquid of density ρ$\rho$ has a hole in its side at a distance y1$y_1$ from the tank's bottom (Fig.) The hole is open to the atmosphere, and its diameter is much smaller than the diameter of the tank. The air above the liquid is maintained at a pressure P. Determine the speed of the liquid as it leaves the hole when the liquid's level is a distance h above the hole.
 
Solution:Because
A2>>A1$A_2>>A_1$, the liquid is approximately at rest at the top of the tank, where the pressure is P. Applying Bernoulli's equation to points 1 and 2 and noting that at the hole P1$P_1$ is equal to atmospheric pressure P0$P_0$, we find that P0+12ρv21+ρgy1=P+ρgy2$P_0+{\displaystyle \frac{1}{2}}\rho v_1^2+\rho g{y}_1=P+\rho g{y}_2$
y2−y1=h$y_2-y_1=h$
v1=2(P−P0)ρ+2gh−−−−−−−−−−−−−−√${\displaystyle v_1=\sqrt{{\displaystyle \frac{2(P-P_0)}{\rho }}+2gh}}$ P>>Po$P>>P_o$
v1=2pρ−−−√${\displaystyle v_1=\sqrt{{\displaystyle \frac{2p}{\rho }}}}$ (so that the term 2gh$2gh$ can be neglected),P=Po$P=P_o$      v1=2gh−−−√$v_1=\sqrt{2gh}$
In other words, for an open tank, the speed of liquid coming out through a
hole a distance h below the surface is equal to that acquired by an
object falling freely through a vertical distance h$h$. This phenomenon is
known as Torricelli's law .

Example

Reaction force due to velocity of efflux

Example: A liquid of density ρ${\displaystyle \rho }$ comes out with a velocity v
from a tank from a hole of area of cross section A. The reaction force exerted by the liquid on the tube is F. Find the value of F?

Solution:
Mass of water coming out of the tank in unit time,
m=ρAv$m=\rho Av$
The change in momentum of this mass of water in unit time (assuming it completely comes to rest after hitting the wall) 
F=mv⟹F=ρAv2$F=mv⟹F=\rho A{v}^2$

Example

Problem on reaction force due to velocity of efflux on a vessel free to move

Example: In a tank a liquid of density ρ$\rho$ is filled. It comes out with a velocity v$v$ from a hole of area of cross-section A$A$. The reaction force exerted by the liquid on the tube is F$F$. If the tank has mass M$M$ and it's free move in the surface, find the acceleration of the tank.

Solution:
Rate of flow of liquid (in meter cube per second)=A×v=Av$=A\times v=Av$
rate of mass transferred (in kg/s)=Av×ρ=Avρ$=Av\times \rho =Av\rho$
rate of momentum transferred by the liquid i.e. F=Avρ×v=Aρv2$F=Av\rho \times v=A\rho v^2$
Acceleration of the tank = F/M$F/M$
or a=Aρv2M$a={\displaystyle \frac{A\rho v^2}{M}}$
 

Example

Principle and Working of Venturimeter

A venturimeter is a device used for measuring the rate of a flow of a fluid flowing through a pipe. It consists of three parts.1. A short converging part. 2. Throat. 3. Diverging part.

Example:
The diagram (fig.) shows a venturimeter, through which water is flowing. The speed of water at X is 2 cm/sec. What is the speed of water at Y (taking g=1000cm/sec2)$g=1000cm/se{c}^2)$ ?

Solution:
px−py=ρ2(v2y−v2x)⇒Δhρg=ρ2(v2y−v2x)⇒Δhg=12(v2y−v2x)⇒0.51×1000=12(v2y−22)⇒1020=v2y−4⇒1024=v2y⇒vy=32cm/s$$\begin{gathered} p_x-p_y=\frac{\rho }{2}(v_y^2-v_x^2) \\ \Rightarrow \mathrm{\Delta }h\rho g=\frac{\rho }{2}(v_y^2-v_x^2) \\ \Rightarrow \mathrm{\Delta }hg=\frac{1}{2}(v_y^2-v_x^2) \\ \Rightarrow 0.51\times 1000=\frac{1}{2}(v_y^2-2^2) \\ \Rightarrow 1020=v_y^2-4 \\ \Rightarrow 1024=v_y^2 \\ \Rightarrow v_y=32cm/s \end{gathered}$$

Example

Application of Bernoulli's equation

Example: A horizontal pipe of non-uniform cross-section allows water to flow
through it with a velocity 1 ms−1${}^{-1}$ when pressure is 50 kPa at a point. If the velocity of flow has to be 2 ms−1${}^{-1}$ at some other point, what will the pressure at that point?

Solution:
Applying Bernoulli's equation at point 1 and point 2,

⇒P1+12ρ1V21=P2+12ρ2V22$\Rightarrow P_1+{\displaystyle \frac{1}{2}}{\rho }_1{V}_1^2=P_2+{\displaystyle \frac{1}{2}}{\rho }_2{V}_2^2$
⇒50×103+12×103(1)2=P2+12×103×4$\Rightarrow 50\times {10}^3+{\displaystyle \frac{1}{2}}\times {10}^3{\left(1\right)}^2=P_2+{\displaystyle \frac{1}{2}}\times {10}^3\times 4$
⇒5×104+500−2000=p2$\Rightarrow 5\times {10}^4+500-2000=p_2$
⇒P2=48.5 kPa$\Rightarrow P_2=48.5kPa$

Example

Combined use of Bernoulli's equation and Continuity Equation

Example: At a point P in a water pipe line the velocity is 1ms−1${}^{-1}$ and the pressure is 3x105${}^5$ pa . At another point Q the area of cross section is half that of at P and the pressure is 5x105${}^5$ pa . What is the difference of heights between P and Q in metre ? ( g =$=$ 10ms−2${}^{-2}$)

Solution:Applying continuity equation across P and QA2V2=A1V1$A_2{V}_2=A_1{V}_1$⇒V2=2ms−1$\Rightarrow V_2=2m{s}^{-1}$
 Using bernouillis theorem across point P and Q,
3×105+12×1000×(1)2+λgh1=λgh2+12×1000×4+5×105$3\times {10}^5+\frac{1}{2}\times 1000\times {\left(1\right)}^2+\lambda g{h}_1=\lambda g{h}_2+\frac{1}{2}\times 1000\times 4+5\times {10}^5$
⇒h1−h2=2000+5×105−3×105−500λg$\Rightarrow h_1-h_2={\displaystyle \frac{2000+5\times {10}^5-3\times {10}^5-500}{\lambda g}}$
So,
Difference in height =2.15m

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14  Page 15  Page 16  Page 17  Page 18