IEMDaily - Video Lecture Notes

Example

Shape of free surface of fluid in a rotating frame

Example: A circular cylinder of radius

R

and height

H

is filled with
water to a height

(2 / 3) H

. It starts rotating about its axis with constantly increasing angular speed.

Solution:The equation of the free surface is

y = \frac{ω^{2} r^{2}}{2 g} + y_{0}

When the free surface touches the brim of the cylinder, the lowest point of the
paraboloid is at a height

H / 3

above the base, as shown in Fig (b).
When the lowest point of the free surface touches the base of the
cylinder, the height of water in the tank must be

H / 2

. It means that
water must spill out.

Definition

Irrotational Flow

Irrotational flow is a flow in which each element of the moving fluid undergoes no net rotation with respect to a chosen coordinate axes from one instant to other.
Example:
A well-known example of irrotational motion is that of the carriages of the Ferris wheel (giant wheel). In a Ferris wheel although each carriage follows a circular path as the wheel revolves, it does not rotate with respect to the earth, as a
result the passengers remain upright and continue to face the same direction.
Rotation of a fluid particle can be caused only by a torque applied by shear
forces on the sides of the particle. Since shear forces are absent in an ideal
fluid, the flow of ideal fluids is essentially irrotational. Generally when the flow is viscid, it also becomes rotational. This is due to the fact that viscosity introduces velocity gradients and introduces distortion and rotation of fluid particles, even though the fluid as a whole need not rotate about a fixed center.

Example

Variation of Pressure in a fluid with constant density in a vertically accelerated frame

Example: If a vessel containing a fluid of density

ρ

upto height h is accelerated vertically downwards with acceleration

a_{o}

then what will be the pressure by fluid at the bottom of vessel?

Solution:Net acceleration downwards, experienced by the fluid =

g - a_{0}

So, Pressure at the bottom while accelaration

(P) = P_{0} + p (g - a_{0}) h

Example

Vertical and Horizontal Variation of Pressure in a fluid accelerated horizontally

Example: A U-tube of base length 'l' filled with the same volume of two liquids
of densities

ρ

and

2 ρ

is moving with an acceleration 'a' on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero, then find the height h?

Solution:
For the given situation, liquid of density

2 ρ

should be behind that of

ρ

.
From the right limb,

P_{A} = P_{a t m} + ρ g h

P_{B} = P_{A} + ρ a \frac{l}{2} = P_{a t m} + ρ g h + ρ a \frac{l}{2}

P_{C} = P_{B} + (2 ρ) a \frac{l}{2} = P_{a t m} + ρ g h + \frac{3}{2} ρ a l

....(i)
But from the left limb,

P_{C} = P_{a t m} + (2 ρ) g h

.....(ii)
From Eqs. (i) and (ii),

P_{a t m} + ρ g h + \frac{3}{2} ρ a l = P_{a t m} + 2 ρ g h

\Rightarrow h = \frac{3 a l}{2 g}

Example

Determining inclination of free surface of a fluid in a uniformly accelerated frame in the horizontal direction

Example: What is the minimum horizontal acceleration of the container so that the pressure at point A of the container becomes atmospheric? (the tank is
of sufficient height)

Solution:
Volume equality gives

2 \times 3 = \frac{1}{2} \times h \times 3 \Rightarrow h = 4 m

∴ t a n θ = \frac{4}{3} = \frac{a}{g} \Rightarrow a = \frac{4}{3} g

(the acceleration vector a and g will also have

θ

as the angle between them)

Definition

Introduction to viscosity

Understanding viscosity:
We know that water flows faster than honey. What makes water flow faster? It is due to a particular property of fluid. This property is called viscosity.Viscosity is simply how thick or thin a fluid is. It shows resistance to flow. Fluid with more viscosity flows slower than fluid with less viscosity. Hence we say that honey is more viscous than water.

Definition

Viscous Force

When a block slides on a table surface a frictional force acts on it. This force acts because there is a relative motion between the bottom surface of the block and the table. A similar concept follows in fluid.
Consider a fluid flowing over a ground surface as shown in the figure. The fluid can be considered to be made up of different layers as shown. The ground holds the layer above it. This layer tries to hold back the layer on top of it and so on. In other words, each layer exerts a force on the layer above it.This force is called viscous force. As the name suggests, this force occurs due to the viscosity of fluid. This force resists the motion of the fluid.

Definition

Velocity Gradient

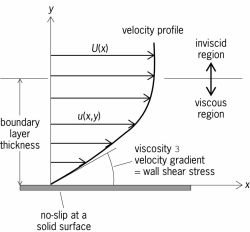
The difference in velocity between adjacent layers of the fluid is known as a velocity gradient and is given by

v / x

, where

v

is the velocity difference and

x

is the distance between the layers.The flow velocity difference between adjacent layers can be measured in terms of velocity gradient. It is given by

u / y

u

= Flow velocity difference between the layers

y

= Distance between the layers

Definition

Coefficient of Viscosity

The ratio of the shearing stress to the velocity gradient is a measure of the viscosity of the fluid and is called the coefficient of viscosity , or = Fx / Av. The cgs unit for measuring the coefficient of viscosity is the poise.

Dimension of coefficient of viscosity is:

[M L^{- 1} T^{- 1}]

Definition

Velocity profile of fluid flowing in a pipe

Suppose a fluid flowing in a pipe. Since the walls of the pipe are stationary, the flow velocity at the wall will be zero. As you go down in the pipe, each layer will try to drag the above layer of fluid. Hence the velocity of the fluid layers till center will increase gradually. The approximate velocity profile can be plotted as follow.