Circular Motion Concepts Page - 1

Definition

Non uniform circular motion

Definition: 
Non- uniform circular motion is defined as the motion of a particle along the circumference of a circle with changing speed. The net acceleration of  particle is inside the circle.

Definition

Non Uniform Circular Motion

In non uniform circular motion magnitude of velocity changes with time.
Direction of the particle changes at every point of time in circular motion.

Definition

Position, Velocity and Acceleration in cartesian coordinate system for uniform circular motion

Position Vector: r⃗ =xi^+yj^$\overrightarrow{r}=x\hat{i}+y\hat{j}$
Velocity Vector: v⃗ =v1i^+v2j^$\overrightarrow{v}=v_1\hat{i}+v_2\hat{j}$
Acceleration Vector: a⃗ =a1i^+a2j^$\overrightarrow{a}=a_1\hat{i}+a_2\hat{j}$

Definition

Position, Velocity and Acceleration Vector

The direction of velocity vector is tangential to the path and its expression is given by the value given in the figure.
The direction of acceleration vector is normal to the path and its expression is given by the value given in the figure.
Here r$r$ is the position vector.

Definition

Radius of Curvature

The radius of a circle which touches a curve at a given point and has the same tangent and curvature at that point. Given above is the formula for radius of curvature for any trajectory

Definition

Angular Acceleration

Angular acceleration is the rate of change of angular velocity. In SI units, it is measured in  rad/s2$rad/s^2$, and is usually denoted by the Greek letter α$\alpha$.

α=dωdt$\alpha ={\displaystyle \frac{d\omega }{dt}}$

Definition

Tangential Acceleration

Tangential acceleration at$a_t$ is the component of acceleration along the tangent in a circular motion. It is a measure of the rate of change of speed along the tangential direction.
a=ΔvΔt$a={\displaystyle \frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}}$

Definition

Angular acceleration

Angular acceleration α$\alpha$:
It is defined as the time rate of change of angular velocity.
α=limδt→0δωδt$\alpha =\underset{\delta t\to 0}{lim}{\displaystyle \frac{\delta \omega }{\delta t}}$
α=dωdt$\alpha ={\displaystyle \frac{d\omega }{dt}}$

Unit of Angular acceleration α$\alpha$ is rads2${\displaystyle \frac{rad}{s^2}}$

Formula

Equations of motion for uniform angular acceleration in circular motion

Equations of motion for uniform angular acceleration are:
ωf=ωi+αt${\omega }_f={\omega }_i+\alpha t$
θ=ωit+12αt2$\theta ={\omega }_{i}t+{\displaystyle \frac{1}{2}}\alpha t^2$
ω2f=ω2i+2αθ${\omega }_f^2={\omega }_i^2+2\alpha \theta$
Example:
A stationary wheel starts rotating about its own axis at uniform angular acceleration 8 rad/s2$8rad/s^2$ . Find the time taken by it to complete 77$77$ rotations.Solution:
From the equations of circular motion, we get:θ=ω0t+12αt2$\theta ={\omega }_{0}t+{\displaystyle \frac{1}{2}}\alpha t^2$
From the given conditions,θ=77×2π rad$\theta =77\times 2\pi rad$, α=8 rad/s2$\alpha =8rad/s^2$ and ω0=0${\omega }_0=0$ as the wheels starts rotating from rest.
So, we get:77×2π=12×8×t2$77\times 2\pi ={\displaystyle \frac{1}{2}}\times 8\times t^2$
or, t=11 s$t=11s$Note:
Particle is at same positions at angular displacement of θ$\theta$ and θ+2nπ$\theta +2n\pi$. 

Formula

Motion of cars on smooth circular banked roads

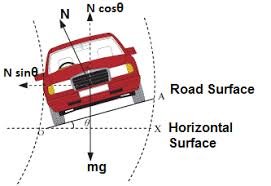
Banking of Road :
For a vehicle to make safe turning on the curved road, the outer edge of the road is raised little above the inner edge making some inclination with the horizontal. This is known as Banking of Road.
Purpose of Banking :With increase in speed of vehicle, the centripetal force required for motion along curved road also increases.
On a plane road, centripetal force is provided by force of friction between tyres and surface of the road. But there is a certain limit beyond which friction can't be further increased.
Therefore, roads are generally banked because here a component of normal also act along with friction to provide necessary centripetal force for higher and safer speed.

On a smooth banked roads, centripetal force will be provided by a component of normal force.
From FBD, we can say that
Ncosθ=Mg$Ncos\theta =Mg$ ........ (1)
Nsinθ=Mv2r$Nsin\theta ={\displaystyle \frac{M{v}^2}{r}}$ ......... (2)
On dividing (2) by (1), we will get tanθ=v2rg$tan\theta ={\displaystyle \frac{v^2}{rg}}$
∴v=rgtanθ−−−−−−√$\therefore v=\sqrt{rgtan\theta }$
This is the maximum speed with which a vehicle can move on a smooth circular banked roads.
P.S. : Here, θ$\theta$ represents angle of banking which is independent of mass of vehicle. 

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5