Circular Motion Concepts Page - 3

Definition

Centrifugal Force

Centrifugal force is a fictitious force that appears in a rotating reference frame. Its direction is opposite to that of the centripetal force i.e. radially outwards from the center. Its magnitude is equal to the centripetal force on the object. Hence, 
F=mv2/R$F={mv}^2/R$
Example: A person sitting in a car feels a force towards right when the car is turning left.
Note: Centrifugal force is a fictitious force. It is only valid inside the rotating frame of reference. For an observer outside, it is no longer valid and the interpretation is different.

Example

Problems on Conical Pendulum

Vertical : Fcosθ=mg$Fcos\theta =mg$
Horizontal  : Fsinθ=mv2r$Fsin\theta ={\displaystyle \frac{m{v}^2}{r}}$
tanθ=v2rg${\displaystyle tan\theta =\frac{v^2}{rg}}$
tanθ=rω2g${\displaystyle tan\theta =\frac{r{\omega }^2}{g}}$
sinθcosθ=λsinθω2g${\displaystyle \frac{sin\theta }{cos\theta }=\frac{\lambda sin\theta {\omega }^2}{g}}$
ω2=gλcosθ${\omega }^2={\displaystyle \frac{g}{\lambda cos\theta }}$
T=2πω=2πλcosθg−−−−−−√$T={\displaystyle \frac{2\pi }{\omega }=2\pi \sqrt{\frac{\lambda cos\theta }{g}}}$

Example

Objects moving in vertical circle with tension as the centripetal force

Example: A mass of 2 kg$2kg$ tied to a string of 1 m$1m$ length is rotating in a vertical circle with a uniform speed of 4 ms−1$4m{s}^{-1}$.Find the position of mass  when tension in the string will be 52 N$52N$.[Take g=10ms−2$g=10m{s}^{-2}$]

Solution:
T−mgsinθ=mv2R$T-mgsin\theta ={\displaystyle \frac{m{v}^2}{R}}$ (θ$\theta$ is the angle from the horizontal line
Thus we get: 52−2×10×sinθ=2×161$52-2\times 10\times sin\theta ={\displaystyle \frac{2\times 16}{1}}$
Thus sinθ=90o$sin\theta ={90}^o$
Thus the tension of 52 N would occur at the bottom most point.

Example

Objects in vertical circle with normal reaction as centripetal force

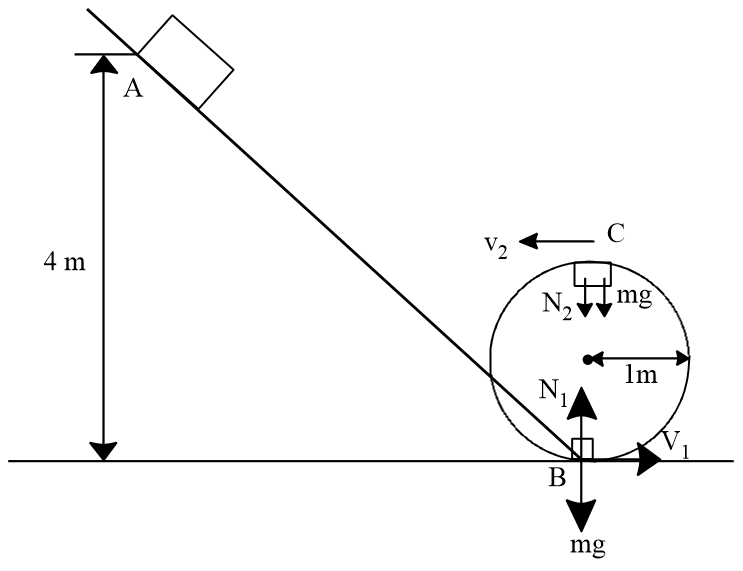
Example: A block is freely sliding down from a vertical height 4 m$4m$ on a smooth inclined plane. The block reaches bottom of inclined plane then it describes vertical circle of radius 1 m$1m$ along smooth track. What is the ratio of normal reactions on the block while it is crossing lowest point and highest point of vertical circle is:

Solution:
Applying the law of conservation of energy at point A and B, we have
mgh=12mv12⇒v1=2gh−−−√⇒v1=8g−−√$$\begin{gathered} mgh={\displaystyle \frac{1}{2}}m{v_1}^2 \\ \Rightarrow v_1=\sqrt{2gh} \\ \Rightarrow v_1=\sqrt{8g} \end{gathered}$$
Now, net force is towards the center is the centripetal force, we have at point B
mv12r=N1−mg${\displaystyle \frac{m{v_1}^2}{r}}=N_1-mg$
⇒N1=mv12r+mg=m(8g)1+mg=9mg$\Rightarrow N_1={\displaystyle \frac{m{v_1}^2}{r}}+mg={\displaystyle \frac{m(8g)}{1}}+mg=9mg$ ..........(I)$(I)$
applying the law of conservation of energy at point B and C, we have
12mv12=mg(2r)+12mv22⇒12m(8g)=mg(2)+12mv22⇒v2=4g−−√$$\begin{gathered} {\displaystyle \frac{1}{2}}m{v_1}^2=mg(2r)+{\displaystyle \frac{1}{2}}m{v_2}^2 \\ \Rightarrow {\displaystyle \frac{1}{2}}m(8g)=mg(2)+{\displaystyle \frac{1}{2}}m{v_2}^2 \\ \Rightarrow v_2=\sqrt{4g} \end{gathered}$$
Now, net force is towards the center is the centripetal force, we have at point C
mv22r=N2+mg${\displaystyle \frac{m{v_2}^2}{r}}=N_2+mg$
⇒N2=mv22r−mg=m(4g)1−mg=3mg$\Rightarrow N_2={\displaystyle \frac{m{v_2}^2}{r}}-mg={\displaystyle \frac{m(4g)}{1}}-mg=3mg$ ..........(II)$(II)$
So the ratio of normal reactions on the block while it is crossing lowest point, highest point of vertical circle is:
N1N2=9mg3mg=3:1${\displaystyle \frac{N_1}{N_2}}={\displaystyle \frac{9mg}{3mg}}=3:1$  ..from (I)$(I)$ and (II)$(II)$

Example

Uniform Circular Motion in Horizontal Plane

Example: A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circular path, and the string makes a constant angle θ$\theta$ with the vertical. The time period rotation of the bob is t and then find the tension T in the thread.

Solution:
Balancing the forces in Horizontal and vertical direction:
Tsinθ=mω2lsinθorT=mω2lTcosθ=mgormω2cosθ=mgorω2=glcosθt=2πω=2πlcosθg−−−−−√T=m[4π2t2]l$$\begin{gathered} Tsin\theta =m{\omega }^{2}lsin\theta orT=m{\omega }^{2}l \\ Tcos\theta =mgor{\displaystyle \frac{m{\omega }^2}{cos\theta }}=mgor{\omega }^2={\displaystyle \frac{g}{lcos\theta }} \\ t={\displaystyle \frac{2\pi }{\omega }}=2\pi \sqrt{{\displaystyle \frac{lcos\theta }{g}}} \\ T=m[{\displaystyle \frac{4{\pi }^2}{t^2}}]l \end{gathered}$$

Example

Problem on Uniform Circular Motion in Horizontal Plane

Example: A vehicle is travelling with uniform speed along a concave road of radius of curvature 19.6 m$19.6m$. At lowest point of concave road if the normal reaction on the vehicle is three times its weight, the speed of vehicle is:

Solution:As normal reaction is three times weight, net force will balance the centripetal force
N−mg=mv2R$N-mg={\displaystyle \frac{m{v}^2}{R}}$
2mg=mv2R$2mg={\displaystyle \frac{m{v}^2}{R}}$
⇒v=2gR−−−−√=2×9.8×19.6−−−−−−−−−−−√$\Rightarrow v=\sqrt{2gR}=\sqrt{2\times 9.8\times 19.6}$
=19.6 ms−1$=19.6m{s}^{-1}$

Example

Uniform Circular Motion in Horizontal Plane with Normal Reaction From a surface as the centripetal force

Example: A particle moving with constant speed u$u$ inside a fixed smooth spherical bowl of radius a$a$ describes a horizontal  circle at a distance a2${\displaystyle \frac{a}{2}}$ below its centre. Then, find u.
Solution:
From the fig., we get:r=a sin 600=a3√2$r=asin{60}^0={\displaystyle \frac{a\sqrt{3}}{2}}$
And the components of normal reaction:
Nsin$Nsin$600=mu2r${60}^0={\displaystyle \frac{m{u}^2}{r}}$
and Ncos$Ncos$600=mg${60}^0=mg$
From the above two equations we get u=31/4ag−−√$u=3^{1/4}\sqrt{ag}$

Example

Problems on Uniform Circular Motion

Example: A body of mass 0.2 kg$0.2kg$ is rotated along a circle of radius 0.5 m$0.5m$ in horizontal plane with uniform speed 3 m/s$3m/s$. The centripetal force on that body is:
Solution: Given, m=0.2 kg$m=0.2kg$, R=0.5 m$R=0.5m$ and v=3 m/s$v=3m/s$
Therefore, Fc=mv2R$F_c={\displaystyle \frac{m{v}^2}{R}}$=(0.2)(32)(0.5)$={\displaystyle \frac{(0.2)(3^2)}{(0.5)}}$=3.6 N

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5