Circular Motion Concepts Page - 4

Example

Accelerated Circular motion in horizontal plane

Example: A small block of mass 1 kg$1kg$ is released from rest at the top of a rough track. The track is a circular arc of radius 40 m$40m$. The block slides along the track without toppling and a frictional force acts on it in the direction opposite to the instantaneous velocity. The work done in overcoming the friction up to the point Q, as shown in the figure, above, is 150 J$150J$. (Take the acceleration due to gravity, g=10 ms−2$g=10m{s}^{-2}$).

Solution:Using work energy theorem we get
mgRsin30o+W=12mv2$mgRsin{30}^o+W={\displaystyle \frac{1}{2}}m{v}^2$
or
200−150=v22$200-150={\displaystyle \frac{v^2}{2}}$
Thus we get v=10 m/s$v=10m/s$
Now, the force equation gives:N−mgcos60o=mv2R$N-mg{\displaystyle \cos {60}^{\mathrm{o}}=\frac{\mathrm{m}{\mathrm{v}}^2}{\mathrm{R}}}$
or, N=5+52=7.5 N${\displaystyle \mathrm{N}=5+\frac{5}{2}=7.5N}$.

Example

Problem on horizontal circle and projectile motion

Example: An open umbrella is held upright and rotated about the handle at a uniform rate of 21 revolution in 44 s44 s. If the rim of the umbrella is a circle of 100 cm100 cm diameter and the height of the rim above ground is 150 cm150 cm, then the drops of water spinning off the rim will hit the ground from center of umbrella, at a distance of:Solution:
Velocity of water drop,
v=rω=0.5×(2π×21)44=1.5 ms−1$v=r\omega =0.5\times {\displaystyle \frac{(2\pi \times 21)}{44}=1.5m{s}^{-1}}$

Time taken to reach ground, t=2hg−−−√=2×1.59.8−−−−−−√=0.55s$t=\sqrt{{\displaystyle \frac{2h}{g}}}=\sqrt{{\displaystyle \frac{2\times 1.5}{9.8}}}=0.55s$

Range of drop, x=vt=1.5×0.55=0.83 m$x=vt=1.5\times 0.55=0.83m$

∴$\therefore$ distance: R=r2+x2−−−−−−√=0.52+0.832−−−−−−−−−−√=0.97 m$R=\sqrt{r^2+x^2}=\sqrt{{0.5}^2+{0.83}^2}=0.97m$=97cm$=97cm$

Example

Problem on centrifugal force

Example:
A car is moving along a circular track of radius 103√$10\sqrt{3}$ m with a constant speed of 36$36$ kmph. A plumb bob is suspended from the roof of the car by a light rigid rod of length 1$1$ m. The angle made by the rod with the track is (g=10ms−2)$(g=10m{s}^{-2})$
Solution:Balancing the forces in the frame of car.
⇒mV2rsinθ=mgcosθ$\Rightarrow {\displaystyle \frac{m{V}^2}{r}}\sin \theta =mg\cos \theta$
tanθ=rgV2$\tan \theta ={\displaystyle \frac{rg}{V^2}}$
        =103√×1010×10=3√$={\displaystyle \frac{10\sqrt{3}\times 10}{10\times 10}}=\sqrt{3}$
⇒θ=60∘$\Rightarrow \theta ={60}^{\circ }$

Example

Variation of centripetal force with radius

Example: Two stones of masses m$m$ and 2 m$2m$ are whirled in horizontal circles, the heavier one in a radius, r2${\displaystyle \frac{r}{2}}$, and the lighter one in radius, r$r$. The tangential speed of lighter stone is n$n$ times that of the value of heavier stone when they experience same centripetal forces. The value of n$n$ is:
Solution:
Centripetal force is same on both as given.
So, mv21r1=2mv22r2${\displaystyle \frac{m{v}_1^2}{r_1}}={\displaystyle \frac{2m{v}_2^2}{r_2}}$
⇒m(nv2)2r=2mv22r2$\Rightarrow {\displaystyle \frac{m(n{v}_2{)}^2}{r}}={\displaystyle \frac{2m{v}_2^2}{{\displaystyle \frac{r}{2}}}}$⇒n2=4$\Rightarrow n^2=4$⇒n=2$\Rightarrow n=2$

Example

Motion in Vertical Circle in which tension becomes zero

Example: A test tube of mass 20 g$20g$ is filled with a gas and fitted with a stopper of 2 g$2g$. It is suspended horizontally by means of a thread of 1 m$1m$ length and heated. When the stopper kicks out, the tube just completes a circle in vertical plane. Find the velocity with which the stopper is kicked out.

Solution: If tubes completes circle
v=5gR−−−−√$v=\sqrt{5gR}$
=5g−−√$=\sqrt{5g}$
Conserving momentum
0=−20×v′+2×v$0=-20\times v^{\prime }+2\times v$
⇒v′=105g−−√$\Rightarrow v^{\prime }=10\sqrt{5g}$
v′=70$v^{\prime }=70$ m/s

Example

Force equations for an object in uniform circular motion

For an object tied on a string rotating in a vertical circle equation for particle's motion will be given by:
1. At the bottom most position:
T=mv2R+mg$T={\displaystyle \frac{m{v}^2}{R}}+mg$

2. At the position 90 degree from vertical line:
T=mv2R$T={\displaystyle \frac{m{v}^2}{R}}$

3. At the top most point of the circle:
T=mv2R−mg$T={\displaystyle \frac{m{v}^2}{R}}-mg$

Result

Limiting condition to complete a vertical circle

The minimum velocity required at the bottom of the circle to complete the vertical circle is:
mv2R−mg=0${\displaystyle \frac{m{v}^2}{R}}-mg=0$
v=Rg−−−√$v=\sqrt{Rg}$
Using energy conservation between topmost and bottommost point of the circle:
mv212=mv22+mg(2R)${\displaystyle \frac{m{v}_1^2}{2}}={\displaystyle \frac{m{v}^2}{2}}+mg(2R)$
This gives:
v1=5gr−−−√$v_1=\sqrt{5gr}$
This is the velocity the topmost point of the circle when v=Rg−−−√$v=\sqrt{Rg}$ is velocity at the bottom.

Definition

Conservation of Energy for an Object in a vertical Circle

Considering level of center of the circle as reference point:
1. Energy at the lowest point of the circle will be:
mv22−mgR${\displaystyle \frac{m{v}^2}{2}}-mgR$
2. Energy at 900${90}^0$ degree from the vertical line of the circle will be:
mv′22${\displaystyle \frac{m{v}^{\prime 2}}{2}}$
3. Energy at the topmost point of the circle will be:
mu22+mgR${\displaystyle \frac{m{u}^2}{2}}+mgR$
 
Since there isn't any energy dissipative force all the energies will be same.

Example

HInge force rigid bodies

Example: A door can just be opened with 10N$10N$ force on the handle of the door. The handle is at a distance of 50cm$50cm$ from the hinges. Then what is the torque applied on the door ( in Nm$Nm$ )?

Solution:The torque would simply be the cross product of the distance and the force applied.
Thus
τ¯=r⃗ ×F⃗ $\overline{\tau }=\overrightarrow{r}\times \overrightarrow{F}$
=(0.5)×(10)$=(0.5)\times (10)$
=5 Nm$=5Nm$

Example

Combination of Vertical Circular Motion and Projectile Motion

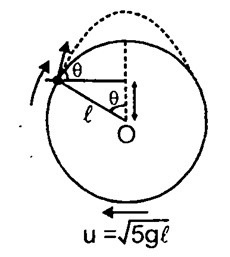
Example: A mass is attached to one end of a mass less string (length l$l$), the other end of which is attached to a fixed support O. The mass swings around in a vertical circle as shown in fig. The mass has the minimum speed (u = 5gl−−−√)$\sqrt{5gl})$ necessary at the lowermost point of the circle to keep the string from going slack. If you cut the string, when it is making angle θ$\theta$ (as shown in figure) with vertical line through centre O of the circle, the resulting projectile motion of the mass has its maximum height located directly above the center of the circle.
Find the value of 10cosθ$10\cos \theta$
Solution:
By conserving energy, mv2/2=0.5m×5gl−mg(l+lcosθ)$m{v}^2/2=0.5m\times 5gl-mg(l+lcos\theta )$⇒v=3gl−2lcosθ−−−−−−−−−−√$\Rightarrow v=\sqrt{3gl-2lcos\theta }$ .
Since the highest point is above the O. So t=lsinθ/vcosθ$t=lsin\theta /vcos\theta$. 
At highest point, final velocity is zero. v=gt$v=gt$solving, θ=600⇒10cosθ=5

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5