Circular Motion Concepts Page - 2

Example

Cars moving on smooth circular banked roads

Question: A circular road of radius r is banked for a speed v=40$v=40$ km/hr. A car of mass m attempts to go on the circular road. The friction coefficient between the tyre and the road is negligible. Then comment on the speed of car when it turns.
Solution:Applying Newton's laws in horizontal and vertical directions. we get
Nsinθ=mv2r$N\sin \theta ={\displaystyle \frac{m{v}^2}{r}}$ ... (I)$(I)$  and Ncosθ=mg$N\cos \theta =mg$  ... (II)$(II)$

from these two equations, we get
tanθ=v2rg$\tan \theta ={\displaystyle \frac{v^2}{rg}}$
v=rgtanθ−−−−−−√$v=\sqrt{rg\tan \theta }$
This is the speed at which the car doesn't slide down even if there is no
friction. Since the car is in horizontal and vertical equilibrium. So the option 'A' is wrong.
If the car's speed is less then the banking speed then It will slip down to reduce the r$r$.

If the car turns at correct speed of 40$40$ m/s. Then the force by the road on the car is given by
N=mv2rsinθ=mgcosθ$N={\displaystyle \frac{m{v}^2}{r\sin \theta }}={\displaystyle \frac{mg}{\cos \theta }}$ ....(III)$(III)$         [from (I)$(I)$  and (II)$(II)$]
By looking at equation (III)$(III)$. we can say that, the force by the road on
the carN$N$ is equal to mv2rsinθ${\displaystyle \frac{m{v}^2}{r\sin \theta }}$, not mv2r${\displaystyle \frac{m{v}^2}{r}}$,
Since θ<π2;⇒sinθ<1&cosθ<1⇒1sinθ>1&1cosθ>1⇒mv2rsinθ>mv2r&mgcosθ>mg⇒N>mv2r&N>mg$$\begin{gathered} \theta <{\displaystyle \frac{\pi }{2}}; \\ \Rightarrow \sin \theta <1\mathrm{\&}\cos \theta <1 \\ \Rightarrow {\displaystyle \frac{1}{\sin \theta }}>1\mathrm{\&}{\displaystyle \frac{1}{\cos \theta }}>1 \\ \Rightarrow {\displaystyle \frac{m{v}^2}{r\sin \theta }}>{\displaystyle \frac{m{v}^2}{r}}\mathrm{\&}{\displaystyle \frac{mg}{\cos \theta }}>mg \\ \Rightarrow N>{\displaystyle \frac{m{v}^2}{r}}\mathrm{\&}N>mg \end{gathered}$$

Formula

Maximum Safe Velocity of a Vehicle on an Unbanked (Plane) Road

Mg$Mg$ = Weight of car 
r$r$ = Radius of curvature of the curve
N1$N_1$ and N2$N_2$ = Normal reaction by ground on two tyres
F1$F_1$ and F2$F_2$ = Frictional force on respective tyres

Hence F1=μN1$F_1=\mu N_1$ and F2=μN2$F_2=\mu N_2$
where μ=$\mu =$ coefficient of friction

In order to move along the curved path, the necessary centripetal force will be provided by total frictional force.
Hence, Mv2r=μ(N1+N2)${\displaystyle \frac{M{v}^2}{r}}=\mu (N_1+N_2)$ ....... (1)
from FBD, N1+N2=Mg$N_1+N_2=Mg$ .......... (2)
from (1) and (2), Mv2r=μMg${\displaystyle \frac{M{v}^2}{r}}=\mu Mg$
∴v=μrg−−−√$\therefore v=\sqrt{\mu rg}$
This is the maximum safe speed with which a vehicle can move along a plane (unbanked) curved road. 

Formula

Motion of Cars on Rough Circular Banked Roads

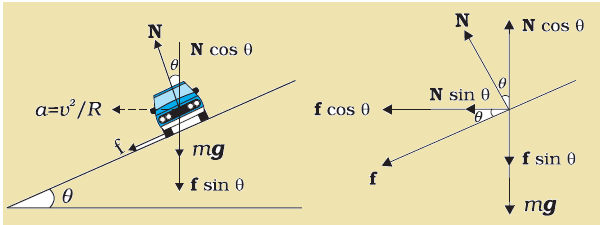
Consider a vehicle of mass m is moving with speed v on a banked road of radius R as shown in the diagram. Let θ$\theta$ be the angle of banking.
N is the normal reaction exerted on the vehicle by banked road.
Let f be the frictional force between the road and the tyres of the vehicle.
From FBD, we can say that,
Total Upward Force = Total Downward Force
Ncosθ=mg+fsinθ$Ncos\theta =mg+fsin\theta$
mg=Ncosθ−fsinθ$mg=Ncos\theta -fsin\theta$ ....... (1)
Horizontal Component Nsinθ$Nsin\theta$ and fcosθ$fcos\theta$ will provide the necessary centripetal force.
mv2R=Nsinθ+fcosθ${\displaystyle \frac{m{v}^2}{R}}=Nsin\theta +fcos\theta$ ........ (2)
On dividing (2) by (1), v2Rg=Nsinθ+fcosθNcosθ−fsinθ${\displaystyle \frac{v^2}{Rg}}={\displaystyle \frac{Nsin\theta +fcos\theta }{Ncos\theta -fsin\theta }}$
But frictional force, f=μN$f=\mu N$ 
where μ=$\mu =$ coefficient of friction between road and tyres. 
v2Rg=Nsinθ+μNcosθNcosθ−μNsinθ${\displaystyle \frac{v^2}{Rg}}={\displaystyle \frac{Nsin\theta +\mu Ncos\theta }{Ncos\theta -\mu Nsin\theta }}$

v2Rg=sinθcosθ+μcosθcosθcosθcosθ−μsinθcosθ${\displaystyle \frac{v^2}{Rg}}={\displaystyle \frac{{\displaystyle \frac{sin\theta }{cos\theta }}+\mu {\displaystyle \frac{cos\theta }{cos\theta }}}{{\displaystyle \frac{cos\theta }{cos\theta }}-\mu {\displaystyle \frac{sin\theta }{cos\theta }}}}$

∴v2Rg=μ+tanθ1−μ tanθ$\therefore {\displaystyle \frac{v^2}{Rg}}={\displaystyle \frac{\mu +tan\theta }{1-\mu tan\theta }}$

v=(μ+tanθ1−μ tanθ)Rg−−−−−−−−−−−−−√$v=\sqrt{({\displaystyle \frac{\mu +tan\theta }{1-\mu tan\theta }})Rg}$
This is the speed with which a vehicle can move safely on a rough circular banked roads.

From this equation we can conclude that :
(1) For a rough plane surface, θ=0$\theta =0$
     v=μRg−−−−√$v=\sqrt{\mu Rg}$
(2) For a smooth banked road, μ=0$\mu =0$
     v=Rg tanθ−−−−−−−√$v=\sqrt{Rgtan\theta }$

Example

Cars moving on circular banked roads with friction acting on tyres

Example: A circular track of radius 300$300$ m is banked at an angle π12${\displaystyle \frac{\pi }{12}}$ radian. If the coefficient of friction between wheel of a car and road is 0.2$0.2$, the maximum safe speed of car is:

Solution:Maximum velocity,
vmax=[(μ+tanθ1−μtanθ)rg]1/2${\displaystyle v_{max}={\left[\left(\frac{\mu +\tan \theta }{1-\mu \tan \theta }\right)rg\right]}^{1/2}}$
=[(0.2+tan15∘1−0.2tan15∘)300×9.8]1/2${\displaystyle ={[\left(\frac{0.2+\tan {15}^{\circ }}{1-0.2\tan {15}^{\circ }}\right)300\times 9.8]}^{1/2}}$
≃38ms−1$\simeq 38m{s}^{-1}$

Formula

Motion of cyclist on circular path

1. A cyclist while going round a curve on a horizontal track has to bend himself a little from his vertical position in order to avoid overturning. When he bends himself inward, a component of the reaction of road provides him the necessary centripetal force for circular motion..

2. In order to find the angle through which a cyclist has to bend himself to take a safe turn, let us assume that

m= combined mass of cycle and cyclist

v= uniform speed with which the cyclist takes the turn

r=radius of circular track

And = angle through which the cyclist bend from vertical

3. Suppose G represents the centre of gravity of the system. If force of friction between the cycle and the road is not taken into account, then following two forces act on the system at the point G.

a) Weight mg of the system acting vertically downloads through the centre of the gravity of the system.

b) Reaction R exerted by the road on the system acting along GR at the angle with the vertical.

4. The reaction R can be resolved into two rectangular components.

a) R cos, acting vertically upwards,

b) R sin, acting horizontally i.e, along the radius and towards the centre of the circular track horizontal component R sin provides the necessary centripetal force. Hence:

Rcos(θ)=mg$R\cos (\theta )=mg$..........(1)

Rsin(θ)=mv2r$R\sin (\theta )={\displaystyle \frac{m{v}^2}{r}}$ ..........(2)

Dividing eq.(2) by eq. (1), we have

θ=tan−1v2rg$\theta =ta{n}^{-1}{\displaystyle \frac{v^2}{rg}}$

Formula

Maximum Safe Velocity of a Vehicle on an Unbanked (Plane) Road

Mg$Mg$ = Weight of car 
r$r$ = Radius of curvature of the curve
N1$N_1$ and N2$N_2$ = Normal reaction by ground on two tyres
F1$F_1$ and F2$F_2$ = Frictional force on respective tyres

Hence F1=μN1$F_1=\mu N_1$ and F2=μN2$F_2=\mu N_2$
where μ=$\mu =$ coefficient of friction

In order to move along the curved path, the necessary centripetal force will be provided by total frictional force.
Hence, Mv2r=μ(N1+N2)${\displaystyle \frac{M{v}^2}{r}}=\mu (N_1+N_2)$ ....... (1)
from FBD, N1+N2=Mg$N_1+N_2=Mg$ .......... (2)
from (1) and (2), Mv2r=μMg${\displaystyle \frac{M{v}^2}{r}}=\mu Mg$
∴v=μrg−−−√$\therefore v=\sqrt{\mu rg}$
This is the maximum safe speed with which a vehicle can move along a plane (unbanked) curved road. 

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5