Optics Concept Page - 5

Example

Kaleidoscope

Kaleidoscope is used to obtain a beautiful pattern of colours. Its principle is based on the multiple image formation by plane mirrors inclined at an angle to each other. It is formed by building a prism with three sides of mirrors. At one end, allow a ray of light to enter with the help of a cardboard piece  with a hole. At  the other end, place a few coloured particles(like bangles) over a glass plate.  

Definition

Construction and Importance of periscope

Construction of Periscope.
A periscope works on the principle of reflection of light from one plane mirror placed at an angle(450${45}^0$) parallel to other plane mirror. Diagram shows the position of mirrors and light rays. In the figure a$a$ and b$b$ are the positions of mirror at an angle of 450${45}^0$.

Importance of periscope : Periscope is used by the submariners to view the objects at the surface of water.

Example

Periscope

Periscopes are used in order to see the objects that are not in direct line of sight. Its working is based on the laws of reflection. It consists of a set of parallel plane mirrors as shown in the diagram. 

Definition

Convergence and divergence of mirrors

If reflected rays converge to a single point after reflection, then this is called as converging behaviour of the mirror . This is observed when a real image is formed. These can be used in applications where all intensity of light is to be focused at a point.
If reflected rays appear to diverge from a single point, then this is called as diverging behaviour of the mirror . This is observed when a virtual image is formed. These can be used in applications where the intensity of light is to be spread over the required region.

Definition

Sign convention

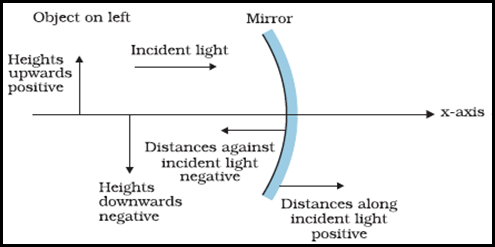
Sign convention is a set of rules to set signs for image distance, object distance, focal length, etc for mathematical analysis of image formation. According to it:

• Object is always placed to the left of mirror
• All distances are measured from the pole of the mirror.
• Distances measured in the direction of the incident ray are positive and the distances measured in the direction opposite to that of the incident rays are negative.
• Distances measured along y-axis above the principal axis are positive and that measured along y-axis below the principal axis are negative.

Note: Sign convention can be reversed and will still give the correct results. 

Result

Relationship between focal length, image distance and object distance for spherical mirrors

The figure shows an object AB at a distance u from the pole of a concave mirror. The image A1B1$A_1{B}_1$ is formed at a distance v from the mirror. The position of the image is obtained by drawing a ray diagram.
Consider the ΔA1CB1$\mathrm{\Delta }{A}_{1}C{B}_1$ and ΔACB$\mathrm{\Delta }ACB$
∠A1CB1=∠ACB$\mathrm{\angle }{A}_{1}C{B}_1=\mathrm{\angle }ACB$ (vertically opposite angles)
∠AB1C=∠ABC$\mathrm{\angle }A{B}_{1}C=\mathrm{\angle }ABC$ (right angles)
∠B1A1C=∠BAC$\mathrm{\angle }{B}_1{A}_{1}C=\mathrm{\angle }BAC$ (third angle will also become equal)
∴ΔA1CB1$\therefore \mathrm{\Delta }{A}_{1}C{B}_1$ and ΔACB$\mathrm{\Delta }ACB$ are similar 
∴ABA1B1=BCB1C$\therefore {\displaystyle \frac{AB}{A_1{B}_1}}={\displaystyle \frac{BC}{B_{1}C}}$
Similarly ΔFB1A1$\mathrm{\Delta }F{B}_1{A}_1$ and ΔFED$\mathrm{\Delta }FED$ are similar
∴EDA1B1=EFFB1$\therefore {\displaystyle \frac{ED}{A_1{B}_1}}={\displaystyle \frac{EF}{F{B}_1}}$
But ED=AB$ED=AB$
ABA1B1=EFFB1${\displaystyle \frac{AB}{A_1{B}_1}}={\displaystyle \frac{EF}{F{B}_1}}$
If D is very close to P then EF = PF
BCB1C=PFFB1${\displaystyle \frac{BC}{B_{1}C}}={\displaystyle \frac{PF}{F{B}_1}}$
BC=PC−PB$BC=PC-PB$
B1C=PB1−PC$B_{1}C=P{B}_1-PC$
FB1=PB1−PF$F{B}_1=P{B}_1-PF$
PC−PBPB1−PC=PFPB1−PF${\displaystyle \frac{PC-PB}{P{B}_1-PC}}={\displaystyle \frac{PF}{P{B}_1-PF}}$
But PC=R,PB=u,PB1=v,PF=f$PC=R,PB=u,P{B}_1=v,PF=f$
Using sign convention, 
PC=−R,PB=−u,PF=−fandPB1=−v$PC=-R,PB=-u,PF=-fandP{B}_1=-v$
So we can equation (3) as :
−R−(−u)−v−(−R)=−f−v−(−f)${\displaystyle \frac{-R-(-u)}{-v-(-R)}}={\displaystyle \frac{-f}{-v-(-f)}}$
−R+u−v+R=−f−v+f${\displaystyle \frac{-R+u}{-v+R}}={\displaystyle \frac{-f}{-v+f}}$
u−RR−v=fv−f${\displaystyle \frac{u-R}{R-v}}={\displaystyle \frac{f}{v-f}}$
uv−uf−Rv+Rf=Rf−vf$uv-uf-Rv+Rf=Rf-vf$
uv−uf−Rv=Rf−Rf−vf$uv-uf-Rv=Rf-Rf-vf$
uv−uf−Rv=−vf$uv-uf-Rv=-vf$
uv−uf−2fv=−vf$uv-uf-2fv=-vf$    (R = 2f)
uv−uf=2fv−fv$uv-uf=2fv-fv$
uv−uf=fv$uv-uf=fv$
Dividing throughout by uvf, we will get :
1f−1v=1u${\displaystyle \frac{1}{f}}-{\displaystyle \frac{1}{v}}={\displaystyle \frac{1}{u}}$
1f=1v+1u${\displaystyle \frac{1}{f}}={\displaystyle \frac{1}{v}}+{\displaystyle \frac{1}{u}}$
This is the required equation. 

Example

Calculate magnification of concave mirror

Problem: 
The image of an object placed in front of a concave mirror of focal length 12 cm is formed at a point which is 10 cm more distant from the mirror than the object. The magnification of the image is:
Solution: We have: 1f=1u+1v${\displaystyle \frac{1}{f}}={\displaystyle \frac{1}{u}}+{\displaystyle \frac{1}{v}}$
Given: f=12 cm$f=12cm$ and v=u+10$v=u+10$
⟹112=1u+1u+10$⟹{\displaystyle \frac{1}{12}}={\displaystyle \frac{1}{u}}+{\displaystyle \frac{1}{u+10}}$
⟹u=20 cm$⟹u=20cm$
⟹v=20+10=30 cm$⟹v=20+10=30cm$
We have magnification, m=vu=3020=1.5$m={\displaystyle \frac{v}{u}}={\displaystyle \frac{30}{20}}=1.5$

Example

Calculate magnification of convex mirror

Problem: 
An object is placed at a distance 2 f from the pole of a convex mirror of focal length f . The linear magnification is:
Solution: 

Here,
u=−2f$u=-2f$
v=$v=$?

1v+1u=1f${\displaystyle \frac{1}{v}}+{\displaystyle \frac{1}{u}}={\displaystyle \frac{1}{f}}$
1v+1−2f=1f${\displaystyle \frac{1}{v}}+{\displaystyle \frac{1}{-2f}}={\displaystyle \frac{1}{f}}$
1v=32f${\displaystyle \frac{1}{v}}={\displaystyle \frac{3}{2f}}$
v=2f3$v={\displaystyle \frac{2f}{3}}$

Now,
M=−vu$M={\displaystyle \frac{-v}{u}}$

=−2f3(−2f)$=-{\displaystyle \frac{{\displaystyle \frac{2f}{3}}}{(-2f)}}$
=13$={\displaystyle \frac{1}{3}}$
(M is positive for convex mirror)

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10  Page 11
Page 12  Page 13  Page 14  Page 15  Page 16  Page 17  Page 18  Page 19  Page 20  Page 21 
Page 22  Page 23  Page 24