Gravitation Concept Page - 2

Definition

Superposition principle and concept of negative mass

According to the principle of superposition in gravitation, net gravitational field at a point is the vector sum of the gravitational fields at that point due to different sources.
Negative mass concept is a technique used to find the gravitational field at a point (say P) easily. If a part of mass is missing from a body, then a body of same mass is assumed to be present on the opposite side of P and at the same distance as original vacancy. Now, the net field is found by calculating field due to the full body without the vacancy and the new assumed mass. 
Example:
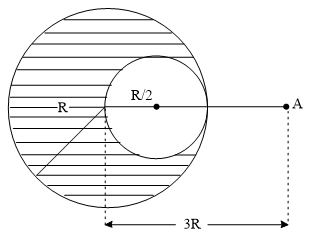
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1$F_1$ on a particle placed at a distance 3R$3R$ from the centre of the sphere. A spherical cavity of radius R2${\displaystyle \frac{R}{2}}$ is now made in the sphere, as shown in the figure. The sphere with cavity now applies a gravitational force F2$F_2$ on the same particle. Find the ratio F2F1${\displaystyle \frac{F_2}{F_1}}$.
Solution:
From super position principle , 
F1=Fr+Fc$F_1=F_r+F_c$
Here Fr=$F_r=$ force due to remaining part =F2$=F_2$
Fc=$F_c=$ force due to mass on the cavity
F1=GMm9R2$F_1={\displaystyle \frac{GMm}{9R^2}}$
Fc=G(M8)m(52R)2=GMm50R2${\displaystyle F_c=\frac{G({\displaystyle \frac{M}{8}})m}{({\displaystyle \frac{5}{2}}R{)}^2}={\displaystyle \frac{GMm}{50R^2}}}$
=≻F2=F1−Fc=GMm9R2−GMm50R2=41GMm450R2$={\displaystyle \succ F_2=F_1-F_c={\displaystyle \frac{GMm}{9R^2}}-{\displaystyle \frac{GMm}{50R^2}}={\displaystyle \frac{41GMm}{450R^2}}}$
=F2F1=4150$={\displaystyle {\displaystyle \frac{F_2}{F_1}}={\displaystyle \frac{41}{50}}}$

Result

Comparision of order of magnitude of gravitational forces with electrical forces

For set of unit charges separated at a distance of 1m, electrostatic force will be:
F=kq1q2r2$F={\displaystyle \frac{k{q}_1{q}_2}{r^2}}$
or F=9×109N$F=9\times {10}^{9}N$
For a set of unit masses separated at a distance of 1m, gravitational force will be:
F=Gm1m2r2$F={\displaystyle \frac{G{m}_1{m}_2}{r^2}}$
or F=6.67×10−11N$F=6.67\times {10}^{-11}N$

From above estimation we can deduce that electrostatic force is way stronger than the gravitational force.  

Example

Freely falling body

A freely falling point object near the surface of earth is acted by a constant gravitational force. This results in a constant acceleration of the falling body. The direction of acceleration due to gravity of freely falling body is always vertically downwards towards the earth. It is usually denoted by g$g$ and its value is given by g=9.8 m/s2$g=9.8m/s^2$ in downward direction.

Definition

Relationship between acceleration due to gravity and gravitational constant

By newton's second law and universal law of gravitation on the surface of earth,
mg=GMmR2$mg={\displaystyle \frac{GMm}{R^2}}$
⟹g=GMR2$⟹g={\displaystyle \frac{GM}{R^2}}$

Definition

Acceleration due to Gravity

Acceleration due to gravity is the acceleration of a body falling freely under the influence of the Earth's gravitational pull at sea level. It is approximately equal to 9.8 m/s2$9.8m/s^2$. Its measured value varies slightly with latitude(due to rotation of earth) and longitude(due to non-spherical shape of earth) and also with depth and height from the earth's surface.  

Example

Variation in time period of pendulum due to change in acceleration due to gravity

Example: A simple pendulum has a time period of T0$T_0$ on the surface of the earth. On another planet whose density is same that of earth but radius is 4$4$ times then time period of this simple pendulum is xT012${\displaystyle \frac{x{T}_0}{12}}$ then what is the value of x$x$?

Solution:
Time period of a simple pendulum is given by
T0=2πLg−−√$T_0=2\pi \sqrt{{\displaystyle \frac{L}{g}}}$
When we go to another planet with different mass, the value of g$g$ changes accordingly.
we have
g=GMR2$g={\displaystyle \frac{GM}{R^2}}$ ; where M$M$ is the mass and R$R$ is radius of the body(planet).
Given, for another planet density is same but the radius is 4 times.
M=density×volume=ρ×43πR3$M=density\times volume=\rho \times {\displaystyle \frac{4}{3}}\pi R^3$
g=G×ρ43πR3R2=G×ρ43πR$g={\displaystyle \frac{G\times \rho {\displaystyle \frac{4}{3}}\pi R^3}{R^2}}=G\times \rho {\displaystyle \frac{4}{3}}\pi R$
here R′=4R$R^{\prime }=4R$
⇒g′=G×ρ43π(4R)=4g$\Rightarrow g^{\prime }=G\times \rho \frac{4}{3}\pi (4R)=4g$
The new time period
T0′=2πL4g−−−√=T0/2${T_0}^{\prime }=2\pi \sqrt{{\displaystyle \frac{L}{4g}}}=T_0/2$
hence x12=12⇒x=6${\displaystyle \frac{x}{12}}={\displaystyle \frac{1}{2}}\Rightarrow x=6$

Formula

Experimental determination of 'g' with the help of simple pendulum

    Experiment
Aim: To measure the acceleration due to gravity using a simple pendulum.

Principle: 
The simple pendulum executes Simple Harmonic Motion (SHM) as the acceleration of the pendulum bob is directly proportional to its displacement from the mean position and is always directed towards it.
Time period 
T=2πLg−−√$T=2\pi \sqrt{{\displaystyle \frac{L}{g}}}$
g=4π2LT2$g=4{\pi }^2{\displaystyle \frac{L}{T^2}}$

Procedure: 
1. Measure the length of the pendulum to the middle of the pendulum bob.
2. Set the pendulum in motion until it completes 'n' to and fro oscillations, taking care to record this time.
T=time for ′n′ oscillationsn$T={\displaystyle \frac{timefor{}^{\prime }{n}^{\prime }oscillations}{n}}$
3. Take 'm' measurements for g using different masses and different values for the length L.

Calculate the value of 'g' using various values of 'T' and 'L'.
 

Definition

Weight and Mass

Weight is the force on an object due to gravity. It is given by W=mg$W=mg$.
Mass is a measure of amount of matter contained in a body. It is a fundamental property of the object and is hence a constant quantity.
Example: A body of mass m=5 kg$m=5kg$ has a weight of W=5×9.8=49 N$W=5\times 9.8=49N$ on the earth's surface.

Definition

equivalence principle in einstein's general relativity

Consider following three conditions to understanding the Equivalence of Inertial and Gravitational mass.

1. let's consider a person standing in spaceship resting on earth. His feet on the floor of the ship. Now we know the normal force is equal to an apparent weight of person which is mg, As acceleration a = 0 (spaceship at rest). Hence normal force = apparent weight = mg.
2. Man in a spaceship which is very far from the planet and he is floating in the ship, hence acceleration a = 0. An apparent weight of man becomes zero (weightlessness).
3. Man in a spaceship which is accelerating with acceleration a = g in space, now the apparent weight of man becomes mg. A spaceship is far away from planet there is no any g due to the planet. But man touching the floor and it gives the normal force to man which give the apparent weight = mg.

Hence the force due to gravity is same as that of acceleration. Hence there is an equivalence between inertial and gravitational mass.

Law

Inertial and Gravitational mass

1) Inertial mass

This is defined by Newton's 2nd law-  F = ma, which states that when a force F is applied to an object, it will accelerate proportionally, and that constant of proportion is the mass of that object. In very concrete terms, to determine the inertial mass, you apply a force of F Newtons to an object, measure the acceleration in m/s2, and F/a will give you the inertial mass m in kilograms.

2) Gravitational mass

This is defined by the force of gravitation, which states that there is a gravitational force between any pair of objects, which is given by

F=Gm1m2r2$F={\displaystyle \frac{G{m}_1{m}_2}{r^2}}$

where G is the universal gravitational constant, m1$m1$ and m2$m2$ are the masses of the two objects, and r is the distance between them. This, in effect defines the gravitational mass of an object.

Gravitational mass is measured by comparing the force of gravity of an unknown mass to the force of gravity of a known mass. This is typically done by balance scale.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10