Gravitation Concept Page - 1

Definition

Gravitational Constant

The gravitational constant (G) is a proportionality constant that appears in the equation for Newton's law of gravitation. The value of G is approximately equal to 6.67×10−11 Nm2kg−2$6.67\times {10}^{-11}N{m}^{2}k{g}^{-2}$. 

Definition

Gravitational unit of force

Some common Gravitational units of force are:

•  kgf: Amount of gravitational force on 1 kg$1kg$ of an object. 1 kgf=9.8 N$1kgf=9.8N$
• gf:  Amount of gravitational force on 1 g$1g$ of an object. 1 gf=9.8×10−3 N$1gf=9.8\times {10}^{-3}N$ 
• N: SI unit of force, force required to accelerate a body of 1 kg by 1 m/s2$1m/s^2$

Result

Characteristics of Gravitational Force

1. It is a universal attractive force.
2. It is directly proportional to the product of the masses of the two bodies.
3. It obeys inverse square law. It is a long range force and does not need any intervening medium for its operation. Gravitational force between two bodies does not depend upon the presence of other bodies.
4. It is the weakest force known in nature. It is a central force (i.e., it acts along the line joining the centres of the two bodies). It is a conservative force (i.e., work done in moving a body against the gravitational force is path independent). Gravitational- force between two bodies is thought to be caused by an exchange of a particle called graviton.

Definition

Universal Law of Gravitation

Newton's law of universal gravitation states that any two bodies in the universe attract each other with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Mathematically, Fg=Gm1m2r2$F_g={\displaystyle \frac{G{m}_1{m}_2}{r^2}}$
where, Fg$F_g$ = Gravitational Force
            G$G$ = Universal Gravitational Constant
            m1, m2$m_1,m_2$ are masses of bodies
            r$r$ = distance between their centre

Definition

Importance of Universal Law of Gravitation

Following are the importance of the universal law of gravitation:

• It explains the force of gravitation acting between two bodies. 
• It describes the phenomenon of revolution of heavenly bodies.
• It determines the downward force on the surface of the earth.

Definition

Force due to gravity

Gravity is the force applied on an object on the surface of earth. It is always directed in the downward direction(i.e. towards the center of earth). It is approximately constant in magnitude. Its value is given by F=mg$F=mg$ where g=9.8 m/s2$g=9.8m/s^2$.

Example

Gravitational force between two objects

For a set masses m1$m_1$ and m2$m_2$ separated at a distance of r$r$, according to Newton's law of gravitation gravitational force will be:
F=Gm1m2r2$F={\displaystyle \frac{G{m}_1{m}_2}{r^2}}$

Example

Understanding Earth's gravitation using universal law of gravitation

A satellite is moving in a circular orbit round the earth. If gravitational pull suddenly disappears,then it moves with the same velocity tangential to original orbit. The reason being, for a body revolving around any object, it is bound by the centripetal force by the object on the body. This force is along the line joining the body and the object. But the velocity of the body will be perpendicular to this force, that is tangential. In this case, when the gravitational force becomes zero, there is no binding on the satellite to revolve around the Earth. Since it was moving with a velocity 'v$v$' in the tangential direction, it continues to move in the same direction with the same velocity 'v$v$' to conserve the momentum.
Example: Keep a stone on a rotating wheel. Stone will fly off the wheel tangential to the wheel's radius.

Example

Problems involving universal law of gravitation

Example: If Fg$F_g$ and Fe$F_e$ are gravitational and electrostatic forces between two electrons at a distance 0.1$0.1$ m$m$ then Fg/Fe$F_g/F_e$
is in what order?

Solution: Gravitational force Fg=Gm2r2$F_g={\displaystyle \frac{G{m}^2}{r^2}}$
Electrostatic force Fe=Kq2r2$F_e={\displaystyle \frac{K{q}^2}{r^2}}$
FgFe=Gm2Kq2${\displaystyle \frac{F_g}{F_e}}={\displaystyle \frac{G{m}^2}{K{q}^2}}$
where G=$G=$Universal gravitational constant and K=1/4πϵ0$K=1/4\pi {ϵ}_0$
G=6.67×10−11$G=6.67\times {10}^{-11}$ and K=9×109$K=9\times {10}^9$
Mass of an electron is 9.31×10−31$9.31\times {10}^{-31}$ and Charge of an electron is 1.6×10−19$1.6\times {10}^{-19}$
Hence, Fg/Fe=Gm2/Kq2$F_g/F_e=G{m}^2/K{q}^2$ is of the order of 10−11−62−9+38=10−43${10}^{-11-62-9+38}={10}^{-43}$

Definition

Experimental method to determine the value of gravitational constant

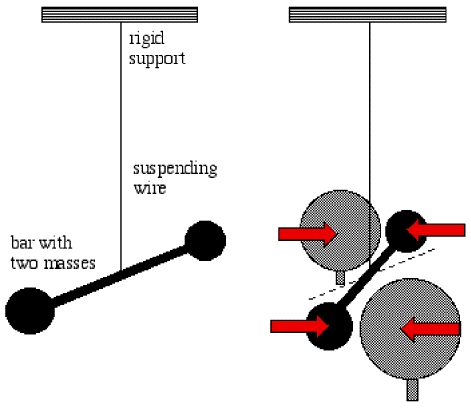
The experimental setup performed by Cavendish is shown in the attached figure. Two masses are attached to the end of a horizontal suspended bar. Then, two large lead spheres are brought close to the small ones but on opposite sides. There is no net force on the bar but a non-zero torque acts on it caused due to gravitational force of attraction. This cause twisting of the suspended wire until a maximum angular displacement. At the point of maximum angular displacement, restoring torque is equal and opposite to the gravitational torque.
GMmd2L=τθ${\displaystyle \frac{GMm}{d^2}}L=\tau \theta$
where τ$\tau$ is the restoring couple per angle of twist and is constant for a given material.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10