IEMDaily - Video Lecture Notes

Definition

Zero vector

A zero or null vector is a vector whose magnitude is 0 and has unspecified arbitrary direction. For example when a body projected vertically from the ground returns to the ground, its vertical displacement is a zero or null vector.

Definition

Triangle Law of Vector addition

Triangle law of vector addition states that when two vectors are represented by two sides of a triangle in magnitude and direction taken in same order then third side of that triangle represents in magnitude and direction the resultant of the two vectors.

Definition

Parallelogram Law of Vector Addition

Parallelogram Law of Vector Addition states that when two vectors are represented by two adjacent sides of a parallelogram by direction and magnitude then the resultant of these vectors is represented in magnitude and direction by the diagonal of the parallelogram starting from the same point.

Example

use of parallelogram method of vector addition

Parallelogram method of vector:
If two vectors acting at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram, then their resultant is represented in magnitude and direction by the diagonal passing through the common tail of the two vectors.

Hence magnitude and direction of resultant can be found by the relation

\vec{R} = \vec{P} + \vec{Q}

R = \sqrt{P^{2} + Q^{2} + 2 P Q c o s θ}

t a n α = \frac{Q s i n θ}{P + Q c o s θ}

Definition

Polygon Law of Vector Addition

Polygon law of vector addition states that if a number of vectors can be represented in magnitude and direction by the sides of a polygon taken in the same order, then their resultant is represented in magnitude and direction by the closing side of the polygon taken in the opposite order.

Definition

Associative, distributive and commutative law of vector addition

Vector addition follows:
1. Associative law:

\vec{A} + (\vec{B} + \vec{C}) = (\vec{A} + \vec{B}) + \vec{C}

2. Commutative law:

\vec{A} + \vec{B} = \vec{B} + \vec{A}

3. Distributive law:

k (\vec{A} + \vec{B}) = k \vec{A} + k \vec{B}

(

k

is a scalar)
Note:
There are two other forms of distributive law-

\vec{A} . (\vec{B} + \vec{C}) = \vec{A} . \vec{B} + \vec{A} . \vec{C}

\vec{A} \times (\vec{B} + \vec{C}) = \vec{A} \times \vec{B} + \vec{A} \times \vec{C}

Diagram

Associative law of vector addition graphically

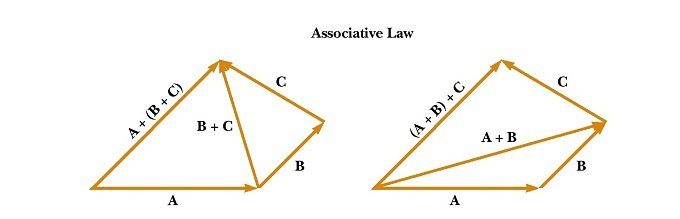
Associative law can be verified graphically as shown in the attached figure.

Example

Calculate magnitude of resultant and angle between two vectors

Example:
What is the angle between

\vec{P}

and the resultant of

(\vec{P} + \vec{Q})

and

(\vec{P} - \vec{Q})

?

Solution:
The resultant of

\vec{P} + \vec{Q}

and

\vec{P} - \vec{Q}

gives

2 \vec{P}

vector which is in the direction of

\vec{P}

Law

Cosine law of vector addition

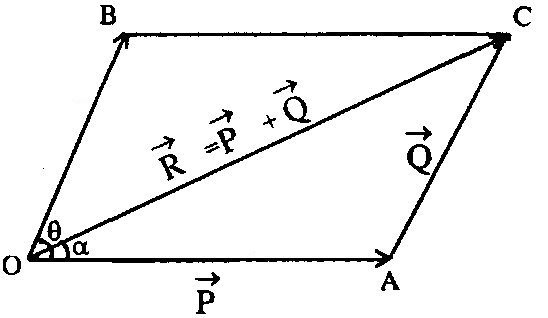
The magnitude and direction of resultant can be found by the relation

\vec{R} = \vec{P} + \vec{Q}

R = \sqrt{P^{2} + Q^{2} + 2 P Q c o s θ}

t a n α = \frac{Q s i n θ}{P + Q c o s θ}

Formula

Law of sines in vector

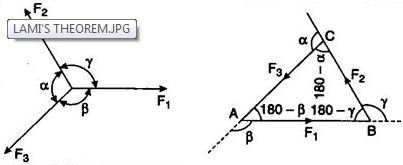
Law of sines:
Law of sines also known as Lamis theorem, which states that if a body is in equilibrium under the action forces, then each force is proportional to the sin of the angle between the other two forces.
Lamis theorem is an equation that relates the magnitudes of three coplanar, concurrent and non-collinear forces, that keeps a body in static equilibrium.