Simple Harmonic Motion Concept Page - 6

Diagram

Plots of potential energy, kinetic energy and total energy v/s position

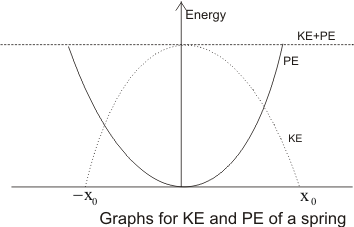
Total energy of an isolated system is constant. 
For mechanical energy,
E=K+U$E=K+U$ 
where E,K,U$E,K,U$ are the total, kinetic and potential energies.
Variation of energies with position for a spring is shown in the attached plot.
Note:
Kinetic energy is always greater than or equal to zero. This property must be satisfied in energy v/s position plot.

Diagram

Plot of potential energy v/s position

F=−dUdx$F=-{\displaystyle \frac{dU}{dx}}$
Force is defined as negative of the slope of potential energy v/s position plot. 
Example:
Consider the given plot defined by the equation:
U=aX22−bX33$U={\displaystyle \frac{a{X}^2}{2}-{\displaystyle \frac{b{X}^3}{3}}}$Between A and B, slope is positive, so force is negative.
Between B and C, slope is negative, so force is positive.
F=−dU/dx=−ax+bx2$F=-dU/dx=-ax+b{x}^2$

Definition

Equilibrium point using potential energy plot

F=−dUdx$F=-{\displaystyle \frac{dU}{dx}}$
If slope of the potential energy v/s position plot is zero, then F=0$F=0$.
For example, in the given plot, B corresponds to the point of equilibrium.

Diagram

Stable and unstable equilibrium points from potential energy plot

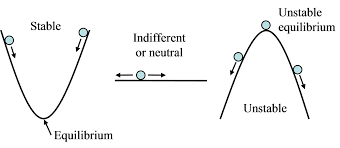
Stable equilibrium means that, with small deviations of the body from this state, forces or moments of forces emerge which tend to return the body to the state of equilibrium. A convex minima (d2Udx2<0${\displaystyle \frac{d^{2}U}{d{x}^2}}<0$) in potential energy v/s position plot refers to a point in unstable equilibrium.
Unstable equilibrium means that, with small deviations of the body from this state, forces or moments of forces emerge which tend to return the body away from the state of equilibrium. A concave maxima (d2Udx2>0${\displaystyle \frac{d^{2}U}{d{x}^2}}>0$) in potential energy v/s position plot refers to a point in unstable equilibrium.

Formula

Equation of Displacement

Equation of displacement:
x=Asin(wt)$x=Asin(wt)$
The amplitude of a particle performing S.H.M. is A$A$. What is the displacement at which its velocity will be half of the maximum velocity?

Solution:
x=Asinωt$x=Asin\omega t$
V=dxdt=Aωcosωt$V={\displaystyle \frac{dx}{dt}}=A\omega cos\omega t$
Vmax=Aω$V_{max}=A\omega$
V=Vmax2=Aωcosωt$V={\displaystyle \frac{V_{max}}{2}}=A\omega cos\omega t$
⇒Aω2=Aωcosωt$\Rightarrow {\displaystyle \frac{A\omega }{2}}=A\omega cos\omega t$
⇒cosωt=12$\Rightarrow cos\omega t={\displaystyle \frac{1}{2}}$
⇒ωt=600$\Rightarrow \omega t={60}^0$
x=Asinωt$x=Asin\omega t$
=Asin600$=Asin{60}^0$
=A3√2$=A{\displaystyle \frac{\sqrt{3}}{2}}$
so, amplitude is 3√A2${\displaystyle \frac{\sqrt{3}A}{2}}$

Example

Displacement as projection of circular motion along a straight line

Example: Figures given correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e.
clockwise or anti-clockwise) are indicated on each figure.Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.

Solution:
(a) Time period, t=2s$t=2s$
Amplitude, A=3cm$A=3cm$
At time, t=0$t=0$, the radius vector OP makes an angle π/2$\pi /2$ with the positive x-axis, i.e., phase angle ϕ=+π/2$\varphi =+\pi /2$
Therefore, the equation of simple harmonic motion for the x-projection of OP, at the time t, is given by the displacement equation:x=Acos[2πtT+ϕ]${\displaystyle x=Acos[{\displaystyle \frac{2\pi t}{T}}+\varphi ]}$    =3cos(2πt2+π2)=−3sin(2πt2)$={\displaystyle 3cos({\displaystyle \frac{2\pi t}{2}}+{\displaystyle \frac{\pi }{2}})=-3sin\left({\displaystyle \frac{2\pi t}{2}}\right)}$∴x=−3sin(πt)cm$\therefore x=-3sin(\pi t)cm$
(b) Time Period, t=4s$t=4s$Amplitude, a=2cm$a=2cm$At time t=0$t=0$, OP makes an angle with the x-axis, in the anticlockwise direction, Hence, phase angle ϕ=+π$\varphi =+\pi$Therefore, the equation of simple harmonic motion for the x-projection of OP, at the time t$t$, is given as:x=acos[2πtT+ϕ]${\displaystyle x=acos[{\displaystyle \frac{2\pi t}{T}}+\varphi ]}$    =2cos(2πt4+π)${\displaystyle =2cos({\displaystyle \frac{2\pi t}{4}}+\pi )}$∴x=−2cos(π2t)m$\therefore {\displaystyle x=-2cos\left({\displaystyle \frac{\pi }{2}}t\right)m}$

Example

Problem on velocity and amplitude of mass attched to spring

Example: A block with mass M$M$ is connected by a mass less spring with stiffness constant k$k$ to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x0$x_0$. Consider two cases: (i) when the block is at x0$x_0$; and (ii) when the block is at x=x0+A$x=x_0+A$. In both the cases, a particle with mass m(<M)$m(<M)$ is softly placed on the block after which they stick to each other.
Which of the following statement(s) is(are) true about the motion after the mass m$m$ is placed on the mass M$M$?

Solution:
In case I,From Conservation of momentum,

MV1=(M+m)V2$M{V}_1=(M+m)V_2$
MV1M+m=V2${\displaystyle \frac{M{V}_1}{M+m}}=V_2$
kM+m−−−−−−−√A2=MM+mkM−−−√A1$\sqrt{{\displaystyle \frac{k}{M+m}}}{A}_2={\displaystyle \frac{M}{M+m}}\sqrt{{\displaystyle \frac{k}{M}}}{A}_1$
A2=MM+m−−−−−−−√A1$A_2=\sqrt{{\displaystyle \frac{M}{M+m}}}{A}_1$
In case II,
A2=A1$A_2=A_1$
T=2πM+mk−−−−−−−√$T=2\pi \sqrt{{\displaystyle \frac{M+m}{k}}}$ in both the cases.
Total energy decreases in first case where as remain same in 2nd case.
Instantaneous speed at x0$x_0$ decreases in both case.

Example

Write force equations of an arrangement of springs in parallel and calculate equivalent spring constant

Example: Two blocks A(5kg)$A(5kg)$ and B(2kg)$B(2kg)$ attached to the ends of a spring constant 1120N/m are placed on a smooth horizontal plane with the spring undeformed. Simultaneously, velocities of 3m/s and 10m/s along the line of the spring in the same direction are imparted to A$A$ and B$B$, then find the maximum extension of the spring.

Solution:
The maximum elongation occurs when the velocity of both the particles becomes equal. Since there is no external force acting in the horizontal direction (for the
blocks + spring system), thus the linear momentum is conserved in horizontal direction:
If the final common velocity is V$V$
5×3+2×10=(5+2)VV=5ms−1$$\begin{gathered} 5\times 3+2\times 10=(5+2)V \\ V=5m{s}^{-1} \end{gathered}$$
Also applying law of conservation of energy for the system (work done by non-conservative force is zero):
Initial Energy =$=$ Final Energy
12×5×32+12×2×102=12×1120x2+12×7×52${\displaystyle \frac{1}{2}}\times 5\times 3^2+{\displaystyle \frac{1}{2}}\times 2\times {10}^2={\displaystyle \frac{1}{2}}\times 1120x^2+{\displaystyle \frac{1}{2}}\times 7\times 5^2$
Solving the above equation we get x=25$x=25$ cm
Also it can be observed that the compression and expansion occur alternately.

Example

Application of conservation of energy for spring in horizontal plane

Example:
A block of mass 2 kg$2kg$ is on a smooth horizontal surface. A light spring of force constant 800 N/m$800N/m$ has one end rigidly attached to a vertical wall and lying on that horizontal surface. Now the block is moved towards the wall compressing the spring over a distance of 5 cm$5cm$ and then suddenly released. By the time the spring regains its natural length and breaks contact with the block, the velocity acquired by the block will be?
Solution:Using conservation of energy
Initial M.E=$M.E=$Final  M.E$M.E$
i.e(P.E)$(P.E)$spring=$=$(K.E)$(K.E)$block
12kx2=12mv2${\displaystyle \frac{1}{2}}k{x}^2={\displaystyle \frac{1}{2}}m{v}^2$
800×25×10−4=2×v2$800\times 25\times {10}^{-4}=2\times v^2$
v=1m/s$v=1m/s$

Example

Time period from force equations

Example:If a particle slides back and forth between two smooth planes as shown in the figure, then find the time period of oscillations if the height is h$h$.
Solution:
By equation of motion
d=ut+12at2$d=ut+{\displaystyle \frac{1}{2}}a{t}^2$
hsinθ=(0)t+12(g sinθ)t2${\displaystyle \frac{h}{sin\theta }}=(0)t+{\displaystyle \frac{1}{2}}(gsin\theta )t^2$
t=2hg sin2θ−−−−−−√=1sinθ2hg−−−√$t=\sqrt{{\displaystyle \frac{2h}{gsi{n}^2\theta }}}={\displaystyle \frac{1}{sin\theta }}\sqrt{{\displaystyle \frac{2h}{g}}}$
So, this much time is taken to reach at bottom from h$h$ height
So, time period will be 4t=4sinθ2hg−−−√$4t={\displaystyle \frac{4}{sin\theta }}\sqrt{{\displaystyle \frac{2h}{g}}}$
So, its is an oscillatory motion with time period 4sinθ2hg−−−√${\displaystyle \frac{4}{sin\theta }}\sqrt{{\displaystyle \frac{2h}{g}}}$ . It is not SHM because force is not proportional to displacement, it is constant of magnitude mg sinθ$mgsin\theta$

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14