Simple Harmonic Motion Concept Page - 12

Example

Solve problems on damped oscillations using small damping approximation

Example: In a damped oscillator with m=500 g$m=500g$, k=100 N/m$k=100N/m$, and b=75 g/s$b=75g/s$, the ratio of the amplitude of the damped oscillations to the initial amplitude at the end of 20$20$ cycles is given as e−x$e^{-x}$. Find x$x$.

Solution:The time period of this system is given by
T=2πmk−−−√=2π0.5100−−−−√=π52√sec$T=2\pi \sqrt{{\displaystyle \frac{m}{k}}}=2\pi \sqrt{{\displaystyle \frac{0.5}{100}}}={\displaystyle \frac{\pi }{5\sqrt{2}}}sec$
For 20$20$ cycles, time taken will be =t=20×π52√=22√πsec$=t=20\times {\displaystyle \frac{\pi }{5\sqrt{2}}}=2\sqrt{2}\pi sec$
So the ratio of amplitude after 20$20$ cycles to that of initial amplitude is
yyo=e−bt2m=e⎛⎝⎜−75×22√π1000⎞⎠⎟=e−0.666${\displaystyle \frac{y}{y_o}}=e^{{\displaystyle \frac{-bt}{2m}}}=e^{(-{\displaystyle \frac{75\times 2\sqrt{2}\pi }{1000}})}=e^{-0.666}$

Formula

Find time period of oscillation assuming small damping

ω=(km−r24m2)−−−−−−−−−−−√$\omega ={\displaystyle \sqrt{(\frac{k}{m}-\frac{r^2}{4m^2})}}$

As w=2πT$w={\displaystyle \frac{2\pi }{T}}$

Example

Find external force in forced oscillation

Example: A simple harmonic oscillator is of mass 0.100 kg$0.100kg$. It is oscillating with a frequency of 5π${\displaystyle \frac{5}{\pi }}$Hz. If its amplitude of vibration is 5$5$ cm, what is the force acting on the particle at its extreme position?

Solution:
F=mw2A$F=m{w}^{2}A$
 ω=2πf=10 rad/sec$\omega =2\pi f=10rad/sec$
F=0.1×100×5100$F=0.1\times 100\times {\displaystyle \frac{5}{100}}$
    =0.5N$=0.5N$ 

Example

Frequency of oscillations in forced oscillations

Example: A 2$2$ kg block hangs without vibrating at the bottom end of a spring with a force constant of 400$400$ N/m. The top end of the spring is attached to the ceiling of an elevator car. The car is rising with an upward acceleration of 5$5$ m/s2${}^2$ when the acceleration suddenly ceases at time t=0$t=0$ and the car moves upward with constant speed (g=10$g=10$ m/s2${}^2$) What is the angular frequency of oscillation of the block after the acceleration ceases?

Solution:
Given :     Mass of the block     m=2kg$m=2kg$    
Spring constant        k=400N/m$k=400N/m$
Let  angular frequency of the oscillation  be   ω$\omega$.
Now using       ω=km−−−√$\omega =\sqrt{{\displaystyle \frac{k}{m}}}$    
ω=4002−−−−√⟹ω=102√ rad/s$\omega =\sqrt{{\displaystyle \frac{400}{2}}}⟹\omega =10\sqrt{2}rad/s$

Definition

Write displacement as a function of time in forced oscillation

The object oscillates about the equilibrium position x0$x_0$.  If we choose the origin of our coordinate system such that x0$x_0$ =0$=0$, then the displacement x$x$ from the equilibrium position as a function of time is given by:x(t)=Acos(wt+ϕ)$x(t)=Acos(wt+\varphi )$

Example

Examples of mechanical resonance

Various examples of mechanical resonance include:
     1. Musical instruments (acoustic resonance).    
     2. Most clocks keep time by mechanical resonance in a balance wheel,   pendulum, or quartz crystal. 
     3. Tidal resonance of the Bay of Fundy.   
     4. Orbital resonance as in some moons of the solar system's gas giants.    
     5. The resonance of the basilar membrane in the ear.    
     6. Making a child's swing, swing higher by pushing it at each swing.    
     7. A wine glass breaking when someone sings a loud note at exactly the right   pitch.

Definition

Oscillations when driving frequency is close to natural frequency

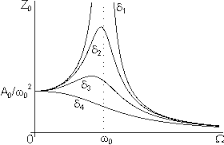
Amplitude of oscillations in shown in the attached plot and given by the formula:
A=Fom20(ω2−ω2d)2+ω2db2−−−−−−−−−−−−−−−−−√$A={\displaystyle \frac{F_o}{\sqrt{m_0^2({\omega }^2-{\omega }_d^2{)}^2+{\omega }_d^2{b}^2}}}$
where
Fo:$F_o:$ Driving Force
mo:$m_o:$ Mass
ω:$\omega :$ Driving Frequency
ωd:${\omega }_d:$ Damping Frequency and b:$b:$ Damping constant

When ω=ωd$\omega ={\omega }_d$, amplitude of oscillations is maximum.
A=Foωdb$A={\displaystyle \frac{F_o}{{\omega }_{d}b}}$ which is a very large value. 

This is the phenomenon of resonance in forced oscillations.

Diagram

Displacement time graph for different oscillations

Definition

Explain maintained oscillation with example

Maintained Oscillation : In maintained oscillation, energy is supplied to the system from outside at the same rate at which the energy is lost by it, so that its amplitude remains constant & the system oscillates with its own natural frequency. Example: Swing, electric tuning fork, balance wheel of a watch, etc

Definition

Free vibrations

The periodic vibrations of a body of constant amplitude in the absence of external force are called free vibrations. Some examples of free vibrations are oscillations of simple pendulum, oscillations of object connected to a horizontal spring, sound produced by tuning fork in short distance, notes of musical instruments, organ pipe, etc.  

Result

Nature of free vibrations

Amplitude and frequency of a freely vibrating body remains constant. They do not lose or gain any energy in the process. Free vibrations for sound can occur only in vacuum. Such vibrations are ideal conditions of oscillations. It is not possible to practically realize free vibrations. 

Definition

Forced vibrations

Vibrations of a body under the constant influence of an external periodic force acting on it are called the forced vibrations. The external applied force is called the driving force. Amplitude of body oscillating under forced oscillations can be decreasing, constant or increasing depending on various factors like difference in amount of driving force and resistive force, difference in frequency of driving force and actual vibrations and difference in phase of driving force and actual vibrations.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14