Mechanical Properties of Matter Concept Page - 4

Diagram

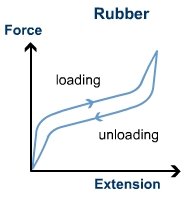
Stress-Strain Curve for Rubbers

Formula

Stress Formula

Longitudinal Stress inside tube = prt${\displaystyle \frac{pr}{t}}$
Where p is internal pressure, r is radius and t is thickness.

Tangential Stress σ$\sigma$ = ForceA${\displaystyle \frac{Force}{A}}$

Definition

Volume Stress

Volume Stress  (or ) Bulk Stress : When a normal stress changes the volume of a body then it is called volume stress. When a solid body is immersed in a fluid, the force at any point is normal to the surface of the body and the magnitude of the force on any small area is proportional to the area i.e., the body is under the action of a pressure P.

 

Volume Stress = ForceArea${\displaystyle \frac{Force}{Area}}$

Definition

Shear Strain

The engineering shear strain is defined as the tangent of that angle, and is equal to the length of deformation at its maximum divided by the perpendicular length in the plane of force application which sometimes makes it easier to calculate.

tanθ$tan\theta$ = DeformationOriginal Length${\displaystyle \frac{Deformation}{OriginalLength}}$

Definition

Volume Strain

It is the ratio of the change in volume of a body to its original volume.
If v$v$ is the original volume of a body and   v+Δv$v+\mathrm{\Delta }v$ is the volume of the body under the action of a normal stress, the change in volume is Δv$\mathrm{\Delta }v$.

Volume Strain = Δvv${\displaystyle \frac{\mathrm{\Delta }v}{v}}$

Definition

Breaking Stress

The stress applied to a material is the force per unit area applied to the material. The maximum stress a material can stand before it breaks is called the breaking stress or ultimate tensile stress. Tensile means the material is under tension.

Example: Find the greatest length of the wire made of material of breaking stress 8 x 108${}^8$N / m2${}^2$ and density 8 x 103${}^3$ kg / m3${}^3$ that can be suspended from a rigid support without breaking.

(g=10m/s2)$(g=10m/s^2)$

Solution:
Stress=length×density×g$Stress=length\times density\times g$
length=stressg×density$length={\displaystyle \frac{stress}{g\times density}}$
=8×10810×8×103$={\displaystyle \frac{8\times {10}^8}{10\times 8\times {10}^3}}$
=104 cm$={10}^{4}cm$
=10 km$=10km$

Example

Stress at a cross-section for a solid in equilibrium

Example: A 20$20$ Kg load is suspended by a wire of cross section 0.4 mm2${}^2$. What is the stress produced in N/m2${}^2$ ?

Solution:stress=ForceappliedunitArea=20×9.810.4×10−6$stress={\displaystyle \frac{Forceapplied}{unitArea}}={\displaystyle \frac{20\times 9.81}{0.4\times {10}^{-6}}}$
=4.9×108N/m2$=4.9\times {10}^{8}N/m^2$

Example

Use of fractional change in length and volume

Example: A uniform cylindrical wire is subjected to a longitudinal tensile stress of 5×107N/m2$5\times {10}^{7}N/m^2$. Young's modulus of the material of the wire is 2×1011N/m2$2\times {10}^{11}N/m^2$. the volume change in the wire is 0.02$0.02$%. find the fractional change in the radius?

Solution: Y=StressΔL/L$Y={\displaystyle \frac{Stress}{\mathrm{\Delta }L/L}}$
or
ΔLL=stressY=5×1072×1011=2.5×10−4${\displaystyle \frac{\mathrm{\Delta }L}{L}}={\displaystyle \frac{stress}{Y}}={\displaystyle \frac{5\times {10}^7}{2\times {10}^{11}}}=2.5\times {10}^{-4}$
Now V=πr2L$V=\pi r^{2}L$
or
ΔVV=πΔ(r2L)πr2L${\displaystyle \frac{\mathrm{\Delta }V}{V}}={\displaystyle \frac{\pi \mathrm{\Delta }(r^{2}L)}{\pi r^{2}L}}$

=r2ΔL+L×2rΔrr2L$={\displaystyle \frac{r^2\mathrm{\Delta }L+L\times 2r\mathrm{\Delta }r}{r^{2}L}}$

ΔLL+2Δrr${\displaystyle \frac{\mathrm{\Delta }L}{L}}+2{\displaystyle \frac{\mathrm{\Delta }r}{r}}$
or
2Δrr=ΔVV−ΔLL$2{\displaystyle \frac{\mathrm{\Delta }r}{r}}={\displaystyle \frac{\mathrm{\Delta }V}{V}}-{\displaystyle \frac{\mathrm{\Delta }L}{L}}$
or
=0.02100−2.5×10−4$={\displaystyle \frac{0.02}{100}}-2.5\times {10}^{-4}$
or
Δrr=1×10−4−2.52×10−4=−0.25×10−4${\displaystyle \frac{\mathrm{\Delta }r}{r}}=1\times {10}^{-4}-{\displaystyle \frac{2.5}{2}}\times {10}^{-4}=-0.25\times {10}^{-4}$

Example

Method to determine Young's Modulus

Method: To find Young's modulus of a wire measure the unstretched length of wire, stretch it using a weight, measure the extension, measure the cross sectional area using a micrometer.
Further by using the formula:
Y=FLδlA$Y={\displaystyle \frac{FL}{\delta lA}}$

Young's Modulus can be determined.

Example

Problems on elasticity where stress in found using equilibrium force analysis

Example: A steel rod of length l1=30cm$l_1=30cm$ and two identical brass rod of length l2=20cm$l_2=20cm$  each support a light horizontal platform as shown in the figure. Cross-sectional area of each of the three rods is A=1cm2$A=1{cm}^2$. A vertically downward force F=5000N$F=5000N$ is applied on the platform. Young's modulus of elasticity for steel Ys=2×1011Nm−2$Y_s=2\times {10}^{11}N{m}^{-2}$ and brass Yb=1×1011Nm−2$Y_b=1\times {10}^{11}N{m}^{-2}$

Solution:
As elongation is given as Δl=Fl/AY⇒F=AYΔl/l$\mathrm{\Delta }l=Fl/AY\Rightarrow F=AY\mathrm{\Delta }l/l$.
 So Fs=AsYsΔls/ls$F_s=A_s{Y}_s\mathrm{\Delta }{l}_s/l_s$
and Fb=AbYbΔlb/lb$F_b=A_b{Y}_b\mathrm{\Delta }{l}_b/l_b$.
Now, Δl$\mathrm{\Delta }l$ is same for all the rods. Adding force on all the rods, Fb+Fs+Fb=F=5000N$F_b+F_s+F_b=F=5000N$
⇒AbYbΔl/lb+AsYsΔl/ls+AbYbΔl/lb=5000 −(1)$\Rightarrow A_b{Y}_b\mathrm{\Delta }l/l_b+A_s{Y}_s\mathrm{\Delta }l/l_s+A_b{Y}_b\mathrm{\Delta }l/l_b=5000-(1)$
As=Ab=1×10−4m2$A_s=A_b=1\times {10}^{-4}{m}^2$
lb=0.2m,ls=0.3m$l_b=0.2m,l_s=0.3m$, Yb=1×1011N/m2;Ys=2×1011N/m2$Y_b=1\times {10}^{11}N/m^2;Y_s=2\times {10}^{11}N/m^2$Using these values in (1)$(1)$,
 Δl=0.03mm$\mathrm{\Delta }l=0.03mm$
So strain in steel rod is Δl/ls=0.03mm/0.3m=10−4$\mathrm{\Delta }l/l_s=0.03mm/0.3m={10}^{-4}$
 As stress=Y×strain=2×1011×10−4=20MPa$stress=Y\times strain=2\times {10}^{11}\times {10}^{-4}=20MPa$

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7