IEMDaily - Video Lecture Notes

Definition

Problems Involving Multiple Blocks

Four rectangular blocks A, B, C and D have masses 2 kg, 3 kg, 5 kg and 10 kg respectively. They are placed on a horizontal surface one over the other with A at the top and D at the bottom in an order. The normal reaction force between C and D will be given by: (take

g = 10 m / s^{2}

)
Forces are resolved as shown in figure .

N_{1} = 20 N

N_{2} = 50 N

N_{3} = 100 N

N_{4} = 200 N

So the Normal force between C and D is

N_{3} = 100 N

Definition

Rate of change of Momentum

Rate of change of linear momentum is defined as force.
F =

\frac{△ P}{△ t}

Example

Pulley-mass system over fixed massless pulleys

The block of mass

m

equal to

100 k g

is being pulled by a horizontal force F

=

2 mg applied to a string as shown in figure

(T a k e g = 10 m / s^{2}) .

The pulley is massless and is fixed at the edge of an immovable table. The value of force exerted by the supporting cable (rod) on the pulley (in Newton)
will be given by:
Let

\underset{T_{1},}{\to} \underset{T_{2}}{\to} a n d \underset{F_{S}}{\to}

be the forces exerted by the horizontal
string, vertical string and the support on the massless pulley
respectively. Then

\underset{T_{1} +}{\to} \underset{T_{2} +}{\to} \underset{F_{S}}{\to} = 0

| \underset{F_{S}}{\to} | = | \underset{T_{1} +}{\to} \underset{T_{2}}{\to} | = 2 \sqrt{2} m g

(∴ T e n s i o n i n e a c h s t r i n g i s | \underset{T_{1}}{\to} | = | \underset{T_{2}}{\to} | = 2 m g)

2 \sqrt{2} m g

Definition

Pulley-mass system with moving pulleys

In the pulley system shown in figure, at an instant if block A is going down at

5 m / s

, block B moves with

5 x m / s

. Then

x

will be:
( In step pulley the ratio of radii is

1 : 2

)
If we analyse each system separately,
Figure shows velocities in each of the string,
Thus comparing the values we get

V_{A} = 8 \times V_{B}

Therefore

x = 8

Definition

Motion of Objects on Fixed Wedges

If block is sliding down on a smooth fixed inclined plane as shown in the figure then net force acting on the wedge due to the block will be given by:
Since

m g

is acting downward and its component along inclined plane is

m g s i n θ

and the normal component is

m g c o s θ

Example

Fixed pulleys on fixed wedges

All the surfaces are frictionless, pulley is light. The triangular block of mass 10 kg is free to move. The acceleration of 10 kg mass would be:

Since both the 24kg and 18kg blocks do-not move.
Horizontal component of force 24 g

= 24 g \sin 37^{0} = 144 N

Horizontal component of force 18 g

= 18 g \sin 53^{0} = 144 N

As the horizontal forces of two blocks are same, the acceleration of the mass 10 kg is

0 m / s^{2} .

Example

Pulley mass system involving moving pulleys and fixed wedges

A cart is being pulled up the incline, using a motor

M

and an ideal pulley and ideal rope arrangement as shown in figure. Then the speed of point

^{'} P^{'}

of the string with which it moves so that the car moves up
the inclined plane with a constant speed of

V_{c a r t} =

2

m/s is:
(Incline is at rest)
We can see that three segments of the string which is supporting the cart is balanced by a single segment of string from motor M. So from pulley constraint relation, for a small displacement, x of string towards motor would produce x' = 3x displacement of cart. Therefore x' = 3x. Differentiating, v' = 3v.
Therefore, velocity of point P

= 3 \times 2 =

6

m/s

Example

Calculate acceleration and tension in string in mass pulley system

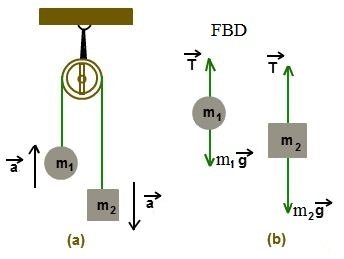
Example: The objects of masses

m_{1} a n d m_{2}

are suspended to two ends of a string which passes through a pulley. Initially this system is at rest. Calculate the acceleration and the tension?
Solution:
Let,
a - acceleration of masses
T- Tension in string
Considering FBD for

m_{1} a n d m_{2}

, we will get equation of motion of masses as

m_{1} a = T - m_{1} g

..........(1)

m_{2} a = m_{2} g - T

..........(2)
solving two equations we get

a = (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) g

T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g

Example

Motion of objects under variable force

Example: A block of mass

m

is connected to a spring ( spring constant k ). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force

F

is applied on the upper end of the spring such that the downward acceleration of the block is given as

a = g - α t,

where

t

is time elapses and

α = 1 m / s^{2},

find the velocity of the point of application of the force.
Solution:
Let the spring to be stretched to

x

at a time

t

, such that

x = x_{b} + x_{f}

where

x_{b}

and

x_{f}

are elongation due to the body,

m

and Force,

F

.

Now, considering the body ,

m g - k x = m a

Or,

m g - k x = m (g - α t)

k x = m α t

Differentiating the above equation, we get

\frac{d (x_{b} + x_{f})}{d t} = \frac{m α}{k}

Or,

v_{b} + v_{f} = \frac{m α}{k} (i)

where

v_{b}

and

v_{f}

are the velocity of body

m

and the point of application of force.
Now, we have

a = g - α t

Or,

\frac{d v_{b}}{d t} = g - α t

Integrating above, we get

\int d v_{b} = \int (g - α t) d t

v_{b} = g t - \frac{α t^{2}}{2} (i i)

From i and ii,

v_{f} = \frac{m α}{k} - g t + \frac{α t^{2}}{2}

(

∵ α = 1

) ,

v_{f} = \frac{m}{k} - g t + \frac{t^{2}}{2}

Example

Length of rod is constant

Consider a rod of length of $l$ resting on a wall and the floor. Its lower end pulled towards left with a constant velocity

V

.As a result the end B starts moving down along the wall. Let us find the velocity of the other end B downward when the rod makes an angle

θ

with the horizontal.
Here the distance between the points is always same, thus the points must have same velocity components in the direction of line joining them i.e, along the length of the rod. If point B is moving downwards with velocity