Centre of Mass, Momentum and Collision Concepts Page - 5

Example

Coefficient of restitution

Definition: The coefficient of restitution (COR) is a measure of the "restitution" of a collision between two objects: how much of the kinetic energy remains for the objects to rebound from one another vs. how much is lost as heat, or work done deforming the objects.

e=Velocity of separationVelocity of Approach$e={\displaystyle \frac{Velocityofseparation}{VelocityofApproach}}$

Example

Conservation of Momentum in inelastic collision

Example: A body of mass 10$10$ g moving with a velocity of 20ms−1$20m{s}^{-1}$ collides with a stationary mass of 90$90$ g. The collision is perfectly inelastic.
Find the percentage loss of kinetic energy of the system.

Solution:
Applying conservation of momentum.
10×20=100×v$10\times 20=100\times v$
v=2$v=2$ m/s
ΔK.E=12×10×(20)2−12×100×(2)2$\mathrm{\Delta }K.E={\displaystyle \frac{1}{2}}\times 10\times (20{)}^2-{\displaystyle \frac{1}{2}}\times 100\times (2{)}^2$
=2000−200$=2000-200$
=1800$=1800$
% loss =180012×10×400×100$={\displaystyle \frac{1800}{{\displaystyle \frac{1}{2}}\times 10\times 400}}\times 100$
=18002000×100=90$={\displaystyle \frac{1800}{2000}}\times 100=90$%

Definition

Elastic collision where one of the mass is very large

Let two masses colliding have mass m1,m2$m_1,m_2$, initial velocities u1,u2$u_1,u_2$ and final velocities v1,v2$v_1,v_2$. Let the collision be in one-dimension. Setting u2=0$u_2=0$ without loss of generality.
Then, using conservation of momentum,
m1v1+m2v2=m1u1$m_1{v}_1+m_2{v}_2=m_1{u}_1$
Using conservation of energy,
m1u21=m1v21+m2v22$m_1{u}_1^2=m_1{v}_1^2+m_2{v}_2^2$
Solving,
v1=m1−m2m1+m2u1$v_1={\displaystyle \frac{m_1-m_2}{m_1+m_2}}{u}_1$
v2=2m1m1+m2u1$v_2={\displaystyle \frac{2m_1}{m_1+m_2}}{u}_1$
Now, since m2>>m1$m_2>>m_1$,
v1≈−u1$v_1\approx -u_1$
v2=0$v_2=0$

Example

One dimensional elastic collision for bodies with equal masses

Question: Two elastic bodies P and Q having equal masses are moving along the same line with velocities of 16$16$ m/s and 10$10$ m/s respectively. What will be their velocities after the elastic collision will be (in m/s)?

Solution:
Let velocities be v1$v_1$ and  v2$v_2$
conservation of  momentum.
m(16+10)=mv1+mv2$m(16+10)=m{v}_1+m{v}_2$
⇒v1+v2=26$\Rightarrow v_1+v_2=26$
e=1$e=1$.
16−10=v2−v1$16-10=v_2-v_1$
The velocities are 10 m/s$10m/s$ and 16 m/s$16m/s$

Example

Velocity of approach and velocity of separation for particles colliding in one dimension

Example: A metal ball falls from a height of 1 m on to a steel plate and jumps upto a height of 81 cm. Find the coefficient of restitution of the ball material.

Solution:Let
u1=$u_1=$Velocity of ball before collision
v1=$v_1=$Velocity of ball after collision
u2=$u_2=$Velocity of plate before collision=0$=0$
v2=$v_2=$Velocity of plate after collision=0$=0$
The coefficient of restitution(e)$(e)$ is given by,   
e=−Velocity of separationVelocity of approach$e=-{\displaystyle \frac{Velocityofseparation}{Velocityofapproach}}$

Velocity  of  separation = v1−v2$v_1-v_2$
Velocity of approach = u1−u2$u_1-u_2$
e=−v1−v2u1−u2$e=-{\displaystyle \frac{v_1-v_2}{u_1-u_2}}$
⇒e=−−v1−0u1−0=v1u1$\Rightarrow e=-{\displaystyle \frac{-v_1-0}{u_1-0}}={\displaystyle \frac{v_1}{u_1}}$

Using v21=2gh1⇒v1=2gh1−−−−√$v_1^2=2g{h}_1\Rightarrow v_1=\sqrt{2g{h}_1}$
Using u21=2gh2⇒u1=2gh2−−−−√$u_1^2=2g{h}_2\Rightarrow u_1=\sqrt{2g{h}_2}$
⇒e=2gh2−−−−√2gh1−−−−√=h2h1−−−√$\Rightarrow e={\displaystyle \frac{\sqrt{2g{h}_2}}{\sqrt{2g{h}_1}}}=\sqrt{{\displaystyle \frac{h_2}{h_1}}}$
Here, h1=100$h_1=100$cm,h2=81$,h_2=81$cm
e=h2h1−−−√=81100−−−−√=0.9$e=\sqrt{{\displaystyle \frac{h_2}{h_1}}}=\sqrt{{\displaystyle \frac{81}{100}}}=0.9$

Example

Conservation of Angular Momentum for perfectly inelastic collision of point mass with rigid body

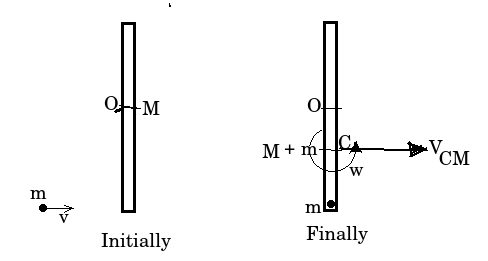
Example: A uniform rod is resting freely over a smooth horizontal plane. A
particle moving horizontally strikes at one end of the rod normally and gets stuck.
Comment on angular momentum of the the system?

Solution:  The centre of mass of the rod lies at O initially and that of the system lies at point C finally.

The system (rod + particle)  moves translationally with linear velocity
VCM$V_{CM}$ and also rotates about its COM (point C) with an angular
velocity w$w$.
Now as net external force is Zero, thus linear momentum is conserved. i.e P=constant$P=constant$Pi=Pf$P_i=P_f$(M+m)VCM=mv$(M+m)V_{CM}=mv$

Hence  COM of system moves translationally with initial momentum of particle.
Also,  Fexternal=0⟹τexternal=0$F_{external}=0⟹{\tau }_{external}=0$ about all points.Thus angular moment of the system is conserved  about all points before and after the collision.Li=Lf$L_i=L_f$              (for all points)

Example

Conservation of momentum in two dimensions

Considering two balls as a system, there isn't any external force acting on them. Momentum will be conserved in either directions along the motion and perpendicular to it.


p¯¯¯1+p¯¯¯2=p¯¯¯′1+p¯¯¯′2${\overline{p}}_1+{\overline{p}}_2={\overline{p}}_1^{\prime }+{\overline{p}}_2^{\prime }$ 
x¯¯¯→mv+0=p¯¯¯′1+p¯¯¯′2$\overline{x}\to mv+0={\overline{p}}_1^{\prime }+{\overline{p}}_2^{\prime }$ y¯¯¯→0+0=p¯¯¯′1+p¯¯¯′2$\overline{y}\to 0+0={\overline{p}}_1^{\prime }+{\overline{p}}_2^{\prime }$ p¯¯¯1x=m|v′1|cosθ${\overline{p}}_{1x}=m|v_1^{\prime }|cos\theta$
p¯¯¯2x=m|v′2|cosϕ${\overline{p}}_{2x}=m|v_2^{\prime }|cos\varphi$
p¯¯¯1y=m|v′1|sinθ${\overline{p}}_{1y}=m|v_1^{\prime }|sin\theta$p¯¯¯1y=m|v′2|sinϕ${\overline{p}}_{1y}=m|v_2^{\prime }|sin\varphi$12mv2=12mv′21+12mv′22$\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_1^{{}^{\prime }2}+\frac{1}{2}m{v}_2^{{}^{\prime }2}$
v2=v′21+v′22$v^2=v_1^{{}^{\prime }2}+v_2^{{}^{\prime }2}$

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9