Work, Energy and Power Concept Page - 6

Example

Problem using conservation of mechanical energy

Example: What is the minimum velocity required to launch a rocket from the surface of Planet Z ? The planet has a mass of M and a radius of R?

Solution:The total energy of an object in orbit = −GMm2r${\displaystyle \frac{-GMm}{2r}}$ It has least energy if r=R$r=R$ i.e. earth surface.
The total energy of object on earth surface = −GMmR${\displaystyle \frac{-GMm}{R}}$
So, the remaining energy is to be provided by kinetic energy = mv22${\displaystyle \frac{m{v}^2}{2}}$
→−GMm2r−−GMmr=mv22$\to {\displaystyle \frac{-GMm}{2r}}-{\displaystyle \frac{-GMm}{r}}={\displaystyle \frac{m{v}^2}{2}}$
So, v = (GMR)0.5$({\displaystyle \frac{GM}{R}}{)}^{0.5}$

Definition

Conservation of Energy

Law of conservation of energy states that energy can neither be created nor be destroyed it can only be transformed from one form to another form. 

Example

Conservation of Mechanical Energy for simple pendulum

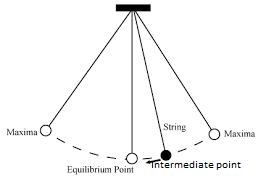
Total mechanical energy is conserved for motion of simple pendulum assuming no losses i.e. Total energy is same at maxima, intermediate point and equilibrium position. Note that total mechanical energy is given as sum of kinetic and potential energy.

Definition

Application of Conservation of Energy

Example

Mass in motion separates in into multiple masses

Example: At a certain height a shell at rest explodes into two equal fragments. One of the fragments receives a horizontal velocity u$u$. The time interval after which, the velocity vectors will be inclined at 120o${120}^o$ to each other is:

Solution:∵$\because$ shell explodes in equal fragments, their masses will be equal,
 by conservation of momentum
2m(0)=mu+mu2$2m(0)=mu+m{u}_2$
∴u2=−u$\therefore u_2=-u$
for angle to be 120∘${120}^{\circ }$
v=v1cos60∘$v=v_{1}cos{60}^{\circ }$
vn=u=v1sin60∘⇒v1=usin60∘$v_n=u=v_1\sin {60}^{\circ }\Rightarrow v_1={\displaystyle \frac{u}{\sin {60}^{\circ }}}$
v=u+at$v=u+at$
v1cos60∘=0+(+g)t⇒usin60∘cos60∘=gt$v_1\cos {60}^{\circ }=0+(+g)t\Rightarrow {\displaystyle \frac{u}{\sin {60}^{\circ }}}cos{60}^{\circ }=gt$
⇒ug1/23√/2=t⇒t=u3√⋅g$\Rightarrow {\displaystyle \frac{u}{g}}{\displaystyle \frac{1/2}{\sqrt{3}/2}}=t\Rightarrow t={\displaystyle \frac{u}{\sqrt{3}\cdot g}}$

Example

Problem on Projectile and its explosion

Question: A projectile is moving at 20 m/s$20m/s$ at its highest point, where it breaks into equal parts due to an internal explosion. One part moves vertically up at 30 m/s$30m/s$ with respect to the ground. Then the other part will move with what velocity?

Solution:
Using momentum conservation,
m×20i^=m/2×30j^+m/2×x$m\times 20\hat{i}=m/2\times 30\hat{j}+m/2\times x$
40i^−30j^=x⇒x=50 m/s$40\hat{i}-30\hat{j}=x\Rightarrow x=50m/s$.

Example

Problems on motion in two dimension where momentum is conserved in one dimension

Example: Two small identical spheres each of mass m$m$ are projected slant-wise from the points A$A$ and B$B$ on the ground with equal velocities u$u$ and making same angles θ$\theta$ and θ$\theta$ as shown in the figure. They collide with each other at the highest point C$C$ of the common path. If the collision is completely inelastic, how much time after the collision the particles come back to the ground?

Solution:
At the highest point, the velocity of the masses will only be horizontal and will be equal to ucosθ$u\cos \theta$.
After the masses stick together, from the principle of
conservation of momentum:
v=mucosθ−mucosθm+m=0$v={\displaystyle \frac{mu\cos \theta -mu\cos \theta }{m+m}}=0$
So the body will be in free fall starting from rest.
For the vertical motion
12gt2=Hmax=u2sin2θ2g${\displaystyle \frac{1}{2}}g{t}^2=H_{max}={\displaystyle \frac{u^2{\sin }^2\theta }{2g}}$
Solving this, we get t=usinθg$t={\displaystyle \frac{u\sin \theta }{g}}$

Example

Momentum conservation of two blocks attached by a spring

Example: A boat of length 10 m$10m$ and mass 450 kg$450kg$ is floating without motion in still water. A man of mass 50 kg$50kg$ standing at one end of it walks to the other end of it and stops. The magnitude of the displacement of the boat in meters relative to ground is:
Solution:
Centre of mass will not be displaced, thus 
m1x1+m2x2=0$m_1{x}_1+m_2{x}_2=0$
Now, let x1=x,thenx2=−(10−x)$Now,let{x}_1=x,then{x}_2=-(10-x)$
(because distance covered by man relative to boat =$=$ 10 m or
x2−(−x1)=10,(in opposite direction)$x_2-(-x_1)=10,\text{(in opposite direction)}$
Thus, 450x−50(10−x)=0orx=1 m$450x-50(10-x)=0orx=1m$

Example

Problems on variable mass system

Example:
Two blocks of masses m1$m_1$ and m2$m_2$ are connected by spring of constant K$K$. The spring is initially compressed and the system is released from rest at t =$=$ 0 second. The work done by spring on the blocks m1$m_1$ and m2$m_2$ be W1$W_1$ and W2$W_2$ respectively by time t$t$. The speeds of both the blocks at time t are non zero. Then find the value of W1W2${\displaystyle \frac{W_1}{W_2}}$ .

Solution:
Let work done by spring on the block of mass m1$m_1$ be W1=$W_1=$ change in kinetic energy 
=12m1v12−12m1(0)2=12m1v12$={\displaystyle {\displaystyle \frac{1}{2}}{m}_1{v_1}^2-{\displaystyle \frac{1}{2}}{m}_1{\left(0\right)}^2={\displaystyle \frac{1}{2}}{m}_1{v_1}^2}$
Similarly, W2=12m2v22$W_2={\displaystyle {\displaystyle \frac{1}{2}}{m}_2{v_2}^2}$
⇒W1W2=12m1v2112m2v22$\Rightarrow {\displaystyle \frac{W_1}{W_2}}={\displaystyle {\displaystyle \frac{{\displaystyle \frac{1}{2}}{m}_1{v}_1^2}{{\displaystyle \frac{1}{2}}{m}_2{v}_2^2}}}$
From conservation of momentum,
m1v1=m2v2$m_1{v}_1=m_2{v}_2$
∴W1W2=v1v2=m2m1$\therefore {\displaystyle {\displaystyle \frac{W_1}{W_2}}={\displaystyle {\displaystyle \frac{v_1}{v_2}}={\displaystyle {\displaystyle \frac{m_2}{m_1}}}}}$

Definition

Application of conservation of energy in spring

Example:
A mass of 0.5 kg$0.5kg$ moving with a speed of 1.5 m/s$1.5m/s$ on a horizontal smooth surface, collides with a nearly weightless spring of force constant k=50 N/m$k=50N/m$. Find the maximum compression of the spring.
Solution:12mv2=12kxm2${\displaystyle \frac{1}{2}m{v}^2=\frac{1}{2}k{x_m}^2}$
∴xm=mk−−−√.v${\displaystyle \therefore x_m=\sqrt{\frac{m}{k}}.v}$
=0.550−−−√×1.5${\displaystyle =\sqrt{\frac{0.5}{50}}\times 1.5}$
=0.15m

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7