Electrostatics Concept Page - 10

Definition

Electric potential

Electric potential (V$V$) at a point is defined as the amount of work done in bringing a unit positive charge from infinity to that point.
Unit of potential is 1 V=1 JC−1$1V=1{JC}^{-1}$.
V=WQ$V=\frac{W}{Q}$
Note: Potential is taken to be zero at infinity and at ground.

Definition

Electric potential energy

Electric potential energy of charge q at a point (in the presence of field due to any charge configuration) is the work done by the external force (equal and opposite to the electric force) in bringing the charge q from infinity to that point.
ΔU=−∫FE.dr$\mathrm{\Delta }U=-\int F_E.dr$

Definition

Potential difference

Potential difference between two points is the work done in moving a unit positive charge between the two points. Its unit is V$V$ (Volts).
VAB=VA−VB=WABQ$V_{AB}=V_A-V_B={\displaystyle \frac{W_{AB}}{Q}}$

Definition

Potential due to a continuous charge

V=14πϵ0∫dqr$V={\displaystyle \frac{1}{4\pi {ϵ}_0}}\int {\displaystyle \frac{dq}{r}}$
where dq$dq$ is the charge of an element of the continuous distribution.

Result

Work done by a given charge

Work done by a charge to move through a potential difference V$V$ is given by W=Q(Vf−Vi)$W=Q(V_f-V_i)$. 
Where Vf$V_f$ = Final potential and Vi$V_i$ = Initial potential

Definition

Energy density of a medium

Energy density is the amount of energy stored in a given system or region of space per unit volume or mass.
we=12D.EJ/m2$w_e={\displaystyle \frac{1}{2}}D.EJ/m^2$
Energy density in an isotropic medium:
we=12ϵ|E|2$w_e={\displaystyle \frac{1}{2}}ϵ|E{|}^2$                     (∵D=ϵE)$(\because D=ϵE)$

Formula

Electric potential due to a point charge

V=Q4πϵ0r$V={\displaystyle \frac{Q}{4\pi {ϵ}_{0}r}}$
where Q$Q$ is a point charge and V$V$ is the potential due it at a point of r distance.

Example

Potential due to a system of charges

An infinite number of charges each equal to 'q' are placed along the X-axis at x=1$x=1$, x=2$x=2$, x=4$x=4$, x=8$x=8$ ..... The potential at the point x = 0 due to this set of charges is

We know V due to charge q =kQr.$={\displaystyle \frac{kQ}{r.}}$
V is a scalar quantity
total potential at 0 is just sum of all charges.
∴V=kq1+kq2+kq4+−−−−$\therefore V={\displaystyle \frac{kq}{1}}+{\displaystyle \frac{kq}{2}}+{\displaystyle \frac{kq}{4}}+----$
=kq(11−12)$=kq({\displaystyle \frac{1}{1-{\displaystyle \frac{1}{2}}}})$ (sum of infinite G.P=a1−r)$G.P={\displaystyle \frac{a}{1-r}})$
V=q4πε02$V={\displaystyle \frac{q}{4\pi {\epsilon }_0}}2$
∴V=2q4πε0$\therefore V={\displaystyle \frac{2q}{4\pi {\epsilon }_0}}$

Formula

Potential due to an infinitely long uniformly charged wire

V=λ4πϵ0ln[(l/2)+(l/2)2+y2−−−−−−−−−√−(l/2)+(l/2)2+y2−−−−−−−−−√]$V={\displaystyle \frac{\lambda }{4\pi {ϵ}_0}}\ln [{\displaystyle \frac{(l/2)+\sqrt{(l/2{)}^2+y^2}}{-(l/2)+\sqrt{(l/2{)}^2+y^2}}}]$
where l$l$ is the length of the wire, and y$y$ is the perpendicular distance from the wire where the potential is calculated

Formula

Potential due to a infinitely charged sheet

V=2πkσx$V=2\pi k\sigma x$
where k=14πϵ0$k={\displaystyle \frac{1}{4\pi {ϵ}_0}}$ , σ$\sigma$ is the surface charge density and x$x$ is the distance from the plate.

Formula

Potential due to a uniformly charged ring

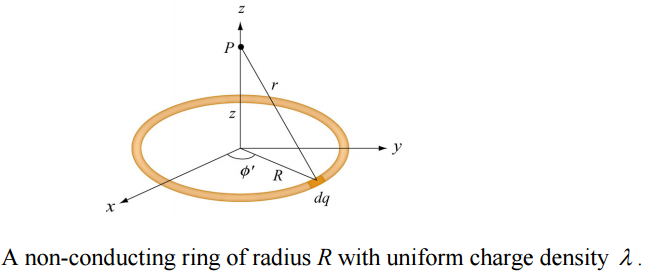
Potential due to uniformly charged ring on its axis:

V=14πϵ0QR2+z2−−−−−−√$V={\displaystyle \frac{1}{4\pi {ϵ}_0}}{\displaystyle \frac{Q}{\sqrt{R^2+z^2}}}$

Formula

Potential due to a uniformly charged disc

V=σ2ϵ0[z2+R2−−−−−−√−z]$V={\displaystyle \frac{\sigma }{2{ϵ}_0}}[\sqrt{z^2+R^2}-z]$
where σ$\sigma$ is the surface charge density

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10
Page 11  Page 12  Page 13  Page 14  Page 15