Example
Equivalent Inductance of infinite inductors in Parallel

By applying KCL in the above circuit we obtain
And since
we have
we have
Definition
Star-delta transformation of inductors

The star and delta circuits shown in the figures are interconvertible.
The equivalent value of inductance for star to delta transformation is:
The equivalent value of inductance for delta to star transformation is:
The equivalent value of inductance for star to delta transformation is:
The equivalent value of inductance for delta to star transformation is:
Definition
Non-ideal inductor

The two contributions to the non-ideal behaviour of inductors are as follows:
- The finite resistance of the wire which is used to wind the coil.
- The cross-turn effects which become important at high frequencies.
Example
Behaviour of RL circuits at the time of switching

Example:
A solenoid of inductance with resistance is connected in parallel to a resistance . A battery of emf and of negligible internal resistance is connected across the parallel combination as shown in the figure. At the time , switch is opened, calculate current through the solenoid after the switch is opened.Solution:
Initially, inductor is fully charged and acts as short circuit. Hence, initially current in the inductor is given by:
When the switch is opened, current across the inductor does not change suddenly.
Hence, current just after opening the switch through the solenoid is given by:
A solenoid of inductance with resistance is connected in parallel to a resistance . A battery of emf and of negligible internal resistance is connected across the parallel combination as shown in the figure. At the time , switch is opened, calculate current through the solenoid after the switch is opened.Solution:
Initially, inductor is fully charged and acts as short circuit. Hence, initially current in the inductor is given by:
When the switch is opened, current across the inductor does not change suddenly.
Hence, current just after opening the switch through the solenoid is given by:
Example
Behaviour of RL circuit in steady state
Example:
A coil of resistance R and inductance L is connected to a battery of e.m.f. E volt. Find the final current in the coil.
Solution:
In steady state, inductor will carry maximum current and it behaves as a short circuit. Hence, the final current is given by:
A coil of resistance R and inductance L is connected to a battery of e.m.f. E volt. Find the final current in the coil.
Solution:
In steady state, inductor will carry maximum current and it behaves as a short circuit. Hence, the final current is given by:
Example
Final value of current in a circuit

Example: In the given figure resistance of coil is zero, find the final value of current in resistor, when plug of key is inserted.
Solution:
In steady state the inductor acts as a component with zero resistance. So the current will not pass through ohm resistor.
Solution:
In steady state the inductor acts as a component with zero resistance. So the current will not pass through ohm resistor.
Example
Multiple resistors and inductors
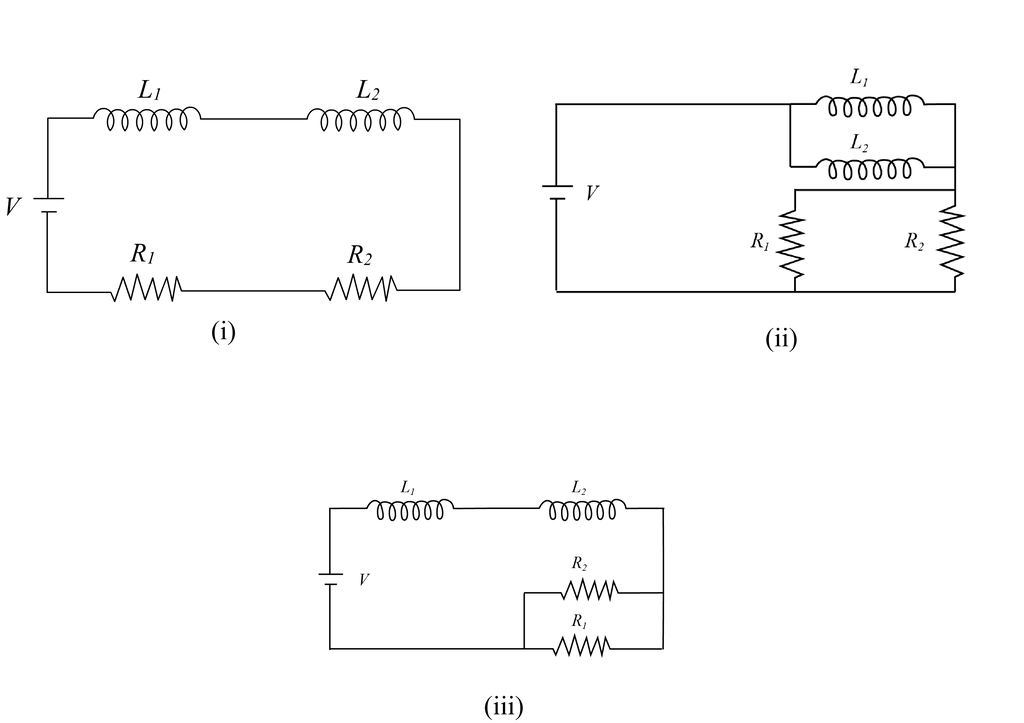
Given
Neglecting mutual inductance, the time constants (in ms) for circuits (i), (ii), and (iii) areFor (i): and
time constant
For (ii): and
time constant
For (iii): and
time constant
Neglecting mutual inductance, the time constants (in ms) for circuits (i), (ii), and (iii) areFor (i): and
time constant
For (ii): and
time constant
For (iii): and
time constant
| BookMarks |
0 Comments
Post a Comment