Magnetism Concept Page - 4

Definition

Deflection of electron due to electric field

The force applied on an electron due to electric field is given by F⃗ =qE⃗ $\overrightarrow{F}=q\overrightarrow{E}$. But the charge on electron is negative. Hence according Newton's second law of motion, electron deflects accelerates opposite to the direction of electric field. 

Example

Example of motion of electron in external magnetic field

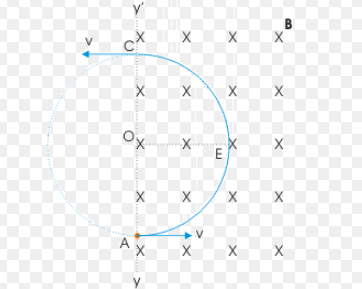
Suppose the magnetic field be downwards as shown in the figure. An electron enters the magnetic field perpendicularly as shown in the figure. Hence according to the right hand thumb rule, the magnetic force on the electron will be (−e)(v⃗ XB⃗ )$(-e)(\overrightarrow{v}X\overrightarrow{B})$. The force will be perpendicular to the motion at every instant. Hence the particle moves in circular motion.

Definition

Deflection of electron due to magnetic field

The force on an electron moving with speed v$v$ in external magnetic field is given by q(v⃗ XB⃗ )$q(\overrightarrow{v}X\overrightarrow{B})$, where q is the charge of the electron and B$B$ be the magnetic field. Hence the force will be perpendicular to the velocity and magnetic field. the direction of the force will be given by right hand thumb rule.

Law

Biot-Savart's Law

According to Biot-Savarts law, the magnitude of the magnetic field dB$dB$ is proportional to the current I$I$, the element length dl$dl$,and inversely proportional to the square of the distance r$r$. Its direction is perpendicular to the plane containing dl$dl$ and r$r$ .Thus, in vector notation,
dB∝Idl×rr3$dB\propto {\displaystyle \frac{Idl\times r}{r^3}}$dB=μ04πIdl×rr3$dB={\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \frac{Idl\times r}{r^3}}$
|dB|=μ04πIdlsinθr2$|dB|={\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \frac{Idlsin\theta }{r^2}}$
where μ04π=10−7Tm/A${\displaystyle \frac{{\mu }_0}{4\pi }}={10}^{-7}Tm/A$ is the constant of proportionality,
μ0${\mu }_0$ is the permeability of free space, 
θ$\theta$ is the angle  between dl$dl$ and the displacement vector r$r$.
Case 1 : When point lies on the conductor
In this condition θ=0orθ=180,havesinθ=0.$\theta =0or\theta =180,havesin\theta =0.$
dB=μ04πIdlsin0r2$dB={\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \frac{Idlsin0}{r^2}}$
Case 2 : When point is perpendicular to the current element
In this condition θ=90$\theta =90$ hence
dB=μ04πIdlsin90r2$dB={\displaystyle \frac{{\mu }_0}{4\pi }}{\displaystyle \frac{Idlsin90}{r^2}}$
Thus it is maximum at this point.

Definition

Comparison between Biot-Savart's Law and Coulomb's Law

Some of the similarities and differences between Biot Savart's Law and Coulomb's Law are:
(i) Both are long range, since both depend inversely on the square of distance from the source to the point of interest. The principle of superposition applies to both fields. [In this connection, note that the magnetic field is linear in the source Idl$Idl$ just as the electrostatic field is linear in its source: the electric charge.]
(ii) The electrostatic field is produced by a scalar source, namely, the electric charge. The magnetic field is produced by a vector source Idl$Idl$.
(iii) The electrostatic field is along the displacement vector joining the source and the field point. The magnetic field is perpendicular to the plane containing the displacement vector r$r$ and the current element Idl$Idl$.
(iv) There is an angle dependence in the Biot-Savart law which is not present in the electrostatic case.

Example

Magnetic field by integrating elemental current carrying sections

A conductor bent into the form of a curve r=$r=$ acosθ(1+sin2θ)${\displaystyle \frac{a}{cos\theta (1+si{n}^2\theta )}}$ in the x-y plane, as shown in the Figure, carries a steady current of 30$30$ A. The magnetic field at O due to current element PP′→$\overrightarrow{P{P}^{\prime }}$ is:

dB=μo4π.idl×r^→r2=μo4π.irdθr2=μo4π.idθr$dB=\frac{{\mu }_o}{4\pi }.i{\displaystyle \frac{\overrightarrow{dl\times \hat{r}}}{r^2}}={\displaystyle \frac{{\mu }_o}{4\pi }}.{\displaystyle \frac{ird\theta }{r^2}}={\displaystyle \frac{{\mu }_o}{4\pi }}.{\displaystyle \frac{id\theta }{r}}$

i.e., dB=μo4π.ia(1+sin2θ)cosθdθ$dB={\displaystyle \frac{{\mu }_o}{4\pi }}.{\displaystyle \frac{i}{a}}(1+{\sin }^2\theta )\cos \theta d\theta$

Hence B = μoi4πa∫π2o(1+sin2θ)d(sinθ)${\displaystyle \frac{{\mu }_{o}i}{4\pi a}}{\int }_o^{{\displaystyle \frac{\pi }{2}}}(1+si{n}^2\theta )d(sin\theta )$

=2μoi4πa[sinθ+sin3θ3]π2o=8μoi12πa$={\displaystyle \frac{2{\mu }_{o}i}{4\pi a}}{[sin\theta +{\displaystyle \frac{si{n}^3\theta }{3}}]}_o^{{\displaystyle \frac{\pi }{2}}}={\displaystyle \frac{8{\mu }_{o}i}{12\pi a}}$

B=23×4π×10−7×30π×1=8×10−6T${\displaystyle \mathrm{B}={\displaystyle \frac{2}{3}}\times {\displaystyle \frac{4\pi \times {10}^{-7}\times 30}{\pi \times 1}}=8\times {10}^{-6}\mathrm{T}}$

Formula

Magnetic field due to a finite straight current carrying wire

A current of 1 A$1A$ is flowing through a straight conductor of length 16 cm$16cm$. The magnetic induction (in tesla) at a point 10 cm$10cm$ from the either end of the wire is: 
B=μ0i4πr(cosθ1+cosθ2)$B={\displaystyle \frac{{\mu }_{0}i}{4\pi r}}(cos{\theta }_1+cos{\theta }_2)$
B=10−7×(1)6×10−2(45+45)$B={\displaystyle \frac{{10}^{-7}\times (1)}{6\times {10}^{-2}}}({\displaystyle \frac{4}{5}}+{\displaystyle \frac{4}{5}})$
   =415×10−5T$={\displaystyle \frac{4}{15}}\times {10}^{-5}T$

Diagram

Magnetic field due to current carrying straight wire

Example

Magnetic field due to different finite wire geometric configurations

Example:
Find the magnetic field at the centre of circular loop in the circuit carrying current I$I$ shown in the figure.

Solution:

Magnetic field due to circular loop is:

B1=μ0I2r=μ0I4πr2π$B_1={\displaystyle \frac{{\mu }_{0}I}{2r}}={\displaystyle \frac{{\mu }_{0}I}{4\pi r}}2\pi$

Field due to straight wire is
B2=μ0I2πr=μ0I4πr2$B_2={\displaystyle \frac{{\mu }_{0}I}{2\pi r}}={\displaystyle \frac{{\mu }_{0}I}{4\pi r}}2$
∵$\because$ net field =B1−B2=μ0I4Ar(2π−2)$=B_1-B_2={\displaystyle \frac{{\mu }_{0}I}{4Ar}}(2\pi -2)$
=μ02π×2IR(π−1)$={\displaystyle \frac{{\mu }_0}{2\pi }}\times {\displaystyle \frac{2I}{R}}(\pi -1)$

Definition

Right hand rule

Grasp the current carrying wire in your right hand with your extended thumb pointing in the direction of the current. Your fingers will curl around in the direction of the magnetic field.

Definition

Right Hand Palm Rule

Right Hand Palm Rule : According to this rule if we open our right hand palm in such a way so that thumb represents the current, 4 fingers represent the magnetic field, then normal to the palm will represents the direction of force.

Definition

Magnetic field due to an infinitely long straight current carrying wire

B=μ0I(2πr)$B={\displaystyle \frac{{\mu }_{0}I}{(2\pi r)}}$ where B$B$ is the magnitude of magnetic field, r$r$ is the distance from the wire where the magnetic field is calculated, and I is the applied current.

BookMarks

Page 1  Page 2  Page 3  Page 4  Page 5  Page 6  Page 7  Page 8  Page 9  Page 10  Page 11
Page 12  Page 13  Page 14  Page 15  Page 16